class mrpt::poses::CPose3D
Overview
A SE(3) pose, comprising a 3D translation and a 3D rotation.
The transformation is stored in two separate containers:
a 3-array for the translation ∈ R³, and
a 3x3 rotation matrix ∈ SO(3).
This class allows parameterizing 6D poses as a 6-vector [x y z yaw pitch roll] (read below for the angles convention). Note however, that the yaw/pitch/roll angles are only computed (on-demand and transparently) when the user requests them. Normally, rotations and transformations are always handled via the 3x3 SO(3) rotation matrix.
Yaw/Pitch/Roll angles are defined as successive rotations around local (dynamic) axes in the Z/Y/X order:
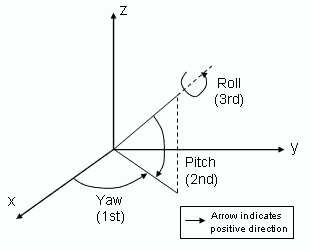



It can be shown that “yaw, pitch, roll” can be also understood as rotations around global (static) axes. Both conventions lead to exactly the same SE(3) transformations, although in it is conventional to write the numbers in reverse order. That is, the same SO(3) rotation can be described equivalently with any of these two parameterizations:
In local axes Z/Y/X convention: [yaw pitch roll] (This is the convention used in mrpt::poses::CPose3D)
In global axes X/Y/Z convention: [roll pitch yaw] (One of the Euler angles conventions)
For further descriptions of point & pose classes, see mrpt::poses::CPoseOrPoint or refer to the 2D/3D Geometry tutorial online.
To change the individual components of the pose, use CPose3D::setFromValues. This class assures that the internal SO(3) rotation matrix is always up-to-date with the “yaw pitch roll” members.
Rotations in 3D can be also represented by quaternions. See mrpt::math::CQuaternion, and method CPose3D::getAsQuaternion.
This class and CPose3DQuat are very similar, and they can be converted to the each other automatically via transformation constructors.
For Lie algebra methods, see mrpt::poses::Lie.
Read also: “A tutorial on SE(3) transformation parameterizations and on-manifold optimization”, in [5]
See also:
CPoseOrPoint, CPoint3D, mrpt::math::CQuaternion
#include <mrpt/poses/CPose3D.h> class CPose3D: public mrpt::poses::CPose, public mrpt::serialization::CSerializable, public mrpt::Stringifyable { public: // typedefs typedef double value_type; typedef double& reference; typedef double const_reference; typedef std::size_t size_type; typedef std::ptrdiff_t difference_type; typedef CPose3D type_value; // enums enum { is_3D_val = 1, }; enum { rotation_dimensions = 3, }; enum { is_PDF_val = 0, }; enum { static_size = 6, }; // fields mrpt::math::CVectorFixedDouble<3> m_coords; // construction CPose3D(); CPose3D( const double x, const double y, const double z, const double yaw = 0, const double pitch = 0, const double roll = 0 ); CPose3D(const math::CMatrixDouble& m); CPose3D(const math::CMatrixDouble44& m); template <class MATRIX33, class VECTOR3> CPose3D( const MATRIX33& rot, const VECTOR3& xyz ); CPose3D(const mrpt::math::CMatrixDouble33& rot, const mrpt::math::CVectorFixedDouble<3>& xyz); CPose3D(const CPose2D& p); CPose3D(const CPoint3D& p); CPose3D(const mrpt::math::TPose3D& o); CPose3D(const mrpt::math::CQuaternionDouble& q, const double x, const double y, const double z); CPose3D(const CPose3DQuat& p); CPose3D(TConstructorFlags_Poses); CPose3D(const mrpt::math::CVectorFixedDouble<12>& vec12); // methods static constexpr size_type size(); static constexpr bool empty(); static constexpr size_type max_size(); static void resize(size_t n); mrpt::math::TPose3D asTPose() const; static CPose3D Identity(); static CPose3D FromXYZYawPitchRoll( double x, double y, double z, double yaw, double pitch, double roll ); static CPose3D FromYawPitchRoll(double yaw, double pitch, double roll); static CPose3D FromTranslation(double x, double y, double z); static CPose3D FromTranslation(const mrpt::math::TPoint3D& t); template <class MATRIX> static CPose3D FromHomogeneousMatrix(const MATRIX& m); template <class MATRIX, class VECTOR> static CPose3D FromRotationAndTranslation( const MATRIX& rot, const VECTOR& t ); static CPose3D FromQuaternion(const mrpt::math::CQuaternionDouble& q); static CPose3D FromQuaternionAndTranslation(const mrpt::math::CQuaternionDouble& q, double x, double y, double z); template <typename Point3DLike> static CPose3D FromQuaternionAndTranslation( const mrpt::math::CQuaternionDouble& q, const Point3DLike& pt ); void getHomogeneousMatrix(mrpt::math::CMatrixDouble44& out_HM) const; void getRotationMatrix(mrpt::math::CMatrixDouble33& ROT) const; const mrpt::math::CMatrixDouble33& getRotationMatrix() const; void setRotationMatrix(const mrpt::math::CMatrixDouble33& ROT); const mrpt::math::TPoint3D translation() const; CPose3D operator + (const CPose3D& b) const; CPoint3D operator + (const CPoint3D& b) const; CPoint3D operator + (const CPoint2D& b) const; void sphericalCoordinates(const mrpt::math::TPoint3D& point, double& out_range, double& out_yaw, double& out_pitch) const; void composePoint( double lx, double ly, double lz, double& gx, double& gy, double& gz, mrpt::optional_ref<mrpt::math::CMatrixDouble33> out_jacobian_df_dpoint = std::nullopt, mrpt::optional_ref<mrpt::math::CMatrixDouble36> out_jacobian_df_dpose = std::nullopt, mrpt::optional_ref<mrpt::math::CMatrixDouble36> out_jacobian_df_dse3 = std::nullopt, bool use_small_rot_approx = false ) const; void composePoint(const mrpt::math::TPoint3D& local_point, mrpt::math::TPoint3D& global_point) const; mrpt::math::TPoint3D composePoint(const mrpt::math::TPoint3D& l) const; void composePoint(const mrpt::math::TPoint3D& local_point, mrpt::math::TPoint2D& global_point) const; void composePoint(double lx, double ly, double lz, float& gx, float& gy, float& gz) const; mrpt::math::TVector3D rotateVector(const mrpt::math::TVector3D& local) const; mrpt::math::TVector3D inverseRotateVector(const mrpt::math::TVector3D& global) const; void inverseComposePoint( const double gx, const double gy, const double gz, double& lx, double& ly, double& lz, mrpt::optional_ref<mrpt::math::CMatrixDouble33> out_jacobian_df_dpoint = std::nullopt, mrpt::optional_ref<mrpt::math::CMatrixDouble36> out_jacobian_df_dpose = std::nullopt, mrpt::optional_ref<mrpt::math::CMatrixDouble36> out_jacobian_df_dse3 = std::nullopt ) const; void inverseComposePoint(const mrpt::math::TPoint3D& g, mrpt::math::TPoint3D& l) const; mrpt::math::TPoint3D inverseComposePoint(const mrpt::math::TPoint3D& g) const; void inverseComposePoint(const mrpt::math::TPoint2D& g, mrpt::math::TPoint2D& l, const double eps = 1e-6) const; void composeFrom(const CPose3D& A, const CPose3D& B); CPose3D& operator += (const CPose3D& b); void inverseComposeFrom(const CPose3D& A, const CPose3D& B); CPose3D operator - (const CPose3D& b) const; void inverse(); void changeCoordinatesReference(const CPose3D& p); void addComponents(const CPose3D& p); void normalizeAngles(); void operator *= (const double s); void setFromValues( const double x0, const double y0, const double z0, const double yaw = 0, const double pitch = 0, const double roll = 0 ); template <typename VECTORLIKE> void setFromXYZQ( const VECTORLIKE& v, size_t index_offset = 0 ); void setYawPitchRoll(const double yaw_, const double pitch_, const double roll_); template <class ARRAYORVECTOR> void setFrom12Vector(const ARRAYORVECTOR& vec12); template <class ARRAYORVECTOR> void getAs12Vector(ARRAYORVECTOR& vec12) const; void getYawPitchRoll(double& yaw, double& pitch, double& roll) const; double yaw() const; double pitch() const; double roll() const; void asVector(vector_t& v) const; void getAsQuaternion(mrpt::math::CQuaternionDouble& q, mrpt::optional_ref<mrpt::math::CMatrixDouble43> out_dq_dr = std::nullopt) const; mrpt::math::CMatrixDouble33 jacobian_rodrigues_from_YPR() const; mrpt::math::CMatrixDouble66 jacobian_pose_rodrigues_from_YPR() const; double operator [] (unsigned int i) const; virtual std::string asString() const; void fromString(const std::string& s); void fromStringRaw(const std::string& s); bool isHorizontal(const double tolerance = 0) const; double distanceEuclidean6D(const CPose3D& o) const; static CPose3D FromString(const std::string& s); CPose3D getOppositeScalar() const; virtual void setToNaN(); const type_value& getPoseMean() const; type_value& getPoseMean(); static constexpr bool is_3D(); static constexpr bool is_PDF(); };
Inherited Members
public: // methods double& x(); double& y(); void x(const double v); void y(const double v); void x_incr(const double v); void y_incr(const double v); const DERIVEDCLASS& derived() const; DERIVEDCLASS& derived();
Typedefs
typedef double value_type
The type of the elements.
typedef CPose3D type_value
Used to emulate CPosePDF types, for example, in mrpt::graphs::CNetworkOfPoses.
Fields
mrpt::math::CVectorFixedDouble<3> m_coords
The translation vector [x,y,z] access directly or with x(), y(), z() setter/getter methods.
Construction
CPose3D()
Default constructor, with all the coordinates set to zero.
CPose3D( const double x, const double y, const double z, const double yaw = 0, const double pitch = 0, const double roll = 0 )
Constructor with Initialization of the pose, translation (x,y,z) in meters, (yaw,pitch,roll) angles in radians.
See also:
CPose3D(const math::CMatrixDouble& m)
Constructor from a 4x4 homogeneous matrix - the passed matrix can be actually of any size larger than or equal 3x4, since only those first values are used (the last row of a homogeneous 4x4 matrix are always fixed).
CPose3D(const math::CMatrixDouble44& m)
Constructor from a 4x4 homogeneous matrix:
template <class MATRIX33, class VECTOR3> CPose3D( const MATRIX33& rot, const VECTOR3& xyz )
Constructor from a 3x3 rotation matrix and a the translation given as a 3-vector, a 3-array, a CPoint3D or a mrpt::math::TPoint3D.
CPose3D(const mrpt::math::CMatrixDouble33& rot, const mrpt::math::CVectorFixedDouble<3>& xyz)
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
CPose3D(const CPose2D& p)
Constructor from a CPose2D object.
CPose3D(const CPoint3D& p)
Constructor from a CPoint3D object.
CPose3D(const mrpt::math::TPose3D& o)
Constructor from lightweight object.
CPose3D(const mrpt::math::CQuaternionDouble& q, const double x, const double y, const double z)
Constructor from a quaternion (which only represents the 3D rotation part) and a 3D displacement.
CPose3D(const CPose3DQuat& p)
Constructor from a CPose3DQuat.
Constructor from a quaternion-based full pose.
CPose3D(TConstructorFlags_Poses)
Fast constructor that leaves all the data uninitialized - call with UNINITIALIZED_POSE as argument.
CPose3D(const mrpt::math::CVectorFixedDouble<12>& vec12)
Constructor from an array with these 12 elements: [r11 r21 r31 r12 r22 r32 r13 r23 r33 tx ty tz] where r{ij} are the entries of the 3x3 rotation matrix and t{x,y,z} are the 3D translation of the pose.
See also:
Methods
static CPose3D Identity()
Returns the identity transformation.
static CPose3D FromXYZYawPitchRoll( double x, double y, double z, double yaw, double pitch, double roll )
Builds a pose from a translation (x,y,z) in meters and (yaw,pitch,roll) angles in radians.
(New in MRPT 2.1.8)
static CPose3D FromYawPitchRoll(double yaw, double pitch, double roll)
Builds a pose with a null translation and (yaw,pitch,roll) angles in radians.
(New in MRPT 2.1.8)
static CPose3D FromTranslation(double x, double y, double z)
Builds a pose with a translation without rotation.
(New in MRPT 2.1.8)
template <class MATRIX> static CPose3D FromHomogeneousMatrix(const MATRIX& m)
Builds a pose with a 4x4 homogeneous matrix.
(New in MRPT 2.1.8)
template <class MATRIX, class VECTOR> static CPose3D FromRotationAndTranslation( const MATRIX& rot, const VECTOR& t )
Builds a pose with a 3x3 SO(3) rotation matrix and a translation vector.
(New in MRPT 2.1.8)
static CPose3D FromQuaternion(const mrpt::math::CQuaternionDouble& q)
Builds a pose from a quaternion (and no translation).
(New in MRPT 2.1.8)
static CPose3D FromQuaternionAndTranslation( const mrpt::math::CQuaternionDouble& q, double x, double y, double z )
Builds a pose from a quaternion and a (x,y,z) translation.
(New in MRPT 2.1.8)
template <typename Point3DLike> static CPose3D FromQuaternionAndTranslation( const mrpt::math::CQuaternionDouble& q, const Point3DLike& pt )
Builds a pose from a quaternion and a 3D translation.
(New in MRPT 2.3.3)
void getHomogeneousMatrix(mrpt::math::CMatrixDouble44& out_HM) const
Returns the corresponding 4x4 homogeneous transformation matrix for the point(translation) or pose (translation+orientation).
See also:
getInverseHomogeneousMatrix, getRotationMatrix
void getRotationMatrix(mrpt::math::CMatrixDouble33& ROT) const
Get the 3x3 rotation matrix.
See also:
const mrpt::math::CMatrixDouble33& getRotationMatrix() const
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
void setRotationMatrix(const mrpt::math::CMatrixDouble33& ROT)
Sets the 3x3 rotation matrix.
See also:
getRotationMatrix, getHomogeneousMatrix
const mrpt::math::TPoint3D translation() const
Returns the (x,y,z) translational part of the SE(3) transformation.
CPose3D operator + (const CPose3D& b) const
The operator \(a \oplus b\) is the pose compounding operator.
CPoint3D operator + (const CPoint3D& b) const
The operator \(a \oplus b\) is the pose compounding operator.
CPoint3D operator + (const CPoint2D& b) const
The operator \(a \oplus b\) is the pose compounding operator.
void sphericalCoordinates( const mrpt::math::TPoint3D& point, double& out_range, double& out_yaw, double& out_pitch ) const
Computes the spherical coordinates of a 3D point as seen from the 6D pose specified by this object.
For the coordinate system see the top of this page.
void composePoint( double lx, double ly, double lz, double& gx, double& gy, double& gz, mrpt::optional_ref<mrpt::math::CMatrixDouble33> out_jacobian_df_dpoint = std::nullopt, mrpt::optional_ref<mrpt::math::CMatrixDouble36> out_jacobian_df_dpose = std::nullopt, mrpt::optional_ref<mrpt::math::CMatrixDouble36> out_jacobian_df_dse3 = std::nullopt, bool use_small_rot_approx = false ) const
An alternative, slightly more efficient way of doing \(G = P \oplus L\) with G and L being 3D points and P this 6D pose.
If pointers are provided, the corresponding Jacobians are returned. “out_jacobian_df_dse3” stands for the Jacobian with respect to the 6D locally Euclidean vector in the tangent space of SE(3). See this report for mathematical details.
Parameters:
If |
set to true, the Jacobian “out_jacobian_df_dpose” uses a fastest linearized appoximation (valid only for small rotations!). |
void composePoint(const mrpt::math::TPoint3D& local_point, mrpt::math::TPoint3D& global_point) const
An alternative, slightly more efficient way of doing \(G = P \oplus L\) with G and L being 3D points and P this 6D pose.
local_point is passed by value to allow global and local point to be the same variable
void composePoint(const mrpt::math::TPoint3D& local_point, mrpt::math::TPoint2D& global_point) const
This version of the method assumes that the resulting point has no Z component (use with caution!)
void composePoint( double lx, double ly, double lz, float& gx, float& gy, float& gz ) const
An alternative, slightly more efficient way of doing \(G = P \oplus L\) with G and L being 3D points and P this 6D pose.
mrpt::math::TVector3D rotateVector(const mrpt::math::TVector3D& local) const
Rotates a vector (i.e.
like composePoint(), but ignoring translation)
mrpt::math::TVector3D inverseRotateVector(const mrpt::math::TVector3D& global) const
Inverse of rotateVector(), i.e.
using the inverse rotation matrix
void inverseComposePoint( const double gx, const double gy, const double gz, double& lx, double& ly, double& lz, mrpt::optional_ref<mrpt::math::CMatrixDouble33> out_jacobian_df_dpoint = std::nullopt, mrpt::optional_ref<mrpt::math::CMatrixDouble36> out_jacobian_df_dpose = std::nullopt, mrpt::optional_ref<mrpt::math::CMatrixDouble36> out_jacobian_df_dse3 = std::nullopt ) const
Computes the 3D point L such as \(L = G \ominus this\).
If pointers are provided, the corresponding Jacobians are returned. “out_jacobian_df_dse3” stands for the Jacobian with respect to the 6D locally Euclidean vector in the tangent space of SE(3). See this report for mathematical details.
See also:
void inverseComposePoint(const mrpt::math::TPoint3D& g, mrpt::math::TPoint3D& l) const
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
void inverseComposePoint(const mrpt::math::TPoint2D& g, mrpt::math::TPoint2D& l, const double eps = 1e-6) const
overload for 2D points
Parameters:
If |
the z component of the result is greater than some epsilon |
void composeFrom(const CPose3D& A, const CPose3D& B)
Makes “this = A (+) B”; this method is slightly more efficient than “this= A + B;” since it avoids the temporary object.
A or B can be “this” without problems.
CPose3D& operator += (const CPose3D& b)
Make \(this = this \oplus b\) (b can be “this” without problems)
void inverseComposeFrom(const CPose3D& A, const CPose3D& B)
Makes \(this = A \ominus B\) this method is slightly more efficient than “this= A - B;” since it avoids the temporary object.
A or B can be “this” without problems.
See also:
CPose3D operator - (const CPose3D& b) const
Compute \(RET = this \oplus b\)
void inverse()
Convert this pose into its inverse, saving the result in itself.
See also:
operator-
void changeCoordinatesReference(const CPose3D& p)
makes: this = p (+) this
void addComponents(const CPose3D& p)
Scalar sum of all 6 components: This is different from poses composition, which is implemented as “+” operators.
See also:
void normalizeAngles()
Rebuild the internal matrix & update the yaw/pitch/roll angles within the ]-PI,PI] range (Must be called after using addComponents)
See also:
void operator *= (const double s)
Scalar multiplication of x,y,z,yaw,pitch & roll (angles will be wrapped to the ]-pi,pi] interval).
void setFromValues( const double x0, const double y0, const double z0, const double yaw = 0, const double pitch = 0, const double roll = 0 )
Set the pose from a 3D position (meters) and yaw/pitch/roll angles (radians) - This method recomputes the internal rotation matrix.
See also:
getYawPitchRoll, setYawPitchRoll
template <typename VECTORLIKE> void setFromXYZQ( const VECTORLIKE& v, size_t index_offset = 0 )
Set the pose from a 3D position (meters) and a quaternion, stored as [x y z qr qx qy qz] in a 7-element vector.
See also:
setFromValues, getYawPitchRoll, setYawPitchRoll, CQuaternion, getAsQuaternion
void setYawPitchRoll(const double yaw_, const double pitch_, const double roll_)
Set the 3 angles of the 3D pose (in radians) - This method recomputes the internal rotation coordinates matrix.
See also:
getYawPitchRoll, setFromValues
template <class ARRAYORVECTOR> void setFrom12Vector(const ARRAYORVECTOR& vec12)
Set pose from an array with these 12 elements: [r11 r21 r31 r12 r22 r32 r13 r23 r33 tx ty tz] where r{ij} are the entries of the 3x3 rotation matrix and t{x,y,z} are the 3D translation of the pose.
See also:
template <class ARRAYORVECTOR> void getAs12Vector(ARRAYORVECTOR& vec12) const
Get the pose representation as an array with these 12 elements: [r11 r21 r31 r12 r22 r32 r13 r23 r33 tx ty tz] where r{ij} are the entries of the 3x3 rotation matrix and t{x,y,z} are the 3D translation of the pose.
See also:
void getYawPitchRoll(double& yaw, double& pitch, double& roll) const
Returns the three angles (yaw, pitch, roll), in radians, from the rotation matrix.
See also:
setFromValues, yaw, pitch, roll
double yaw() const
Get the YAW angle (in radians)
See also:
double pitch() const
Get the PITCH angle (in radians)
See also:
double roll() const
Get the ROLL angle (in radians)
See also:
void asVector(vector_t& v) const
Returns a 6x1 vector with [x y z yaw pitch roll]’.
void getAsQuaternion(mrpt::math::CQuaternionDouble& q, mrpt::optional_ref<mrpt::math::CMatrixDouble43> out_dq_dr = std::nullopt) const
Returns the quaternion associated to the rotation of this object (NOTE: XYZ translation is ignored)
With : \(\phi = roll\), \(\theta = pitch\) and \(\psi = yaw\).
Parameters:
out_dq_dr |
If provided, the 4x3 Jacobian of the transformation will be computed and stored here. It’s the Jacobian of the transformation from (yaw pitch roll) to (qr qx qy qz). |
virtual std::string asString() const
Returns a human-readable textual representation of the object (eg: “[x y z yaw pitch roll]”, angles in degrees.)
See also:
void fromString(const std::string& s)
Set the current object value from a string generated by ‘asString’ (eg: “[x y z yaw pitch roll]”, angles in deg.
)
Parameters:
std::exception |
On invalid format |
See also:
void fromStringRaw(const std::string& s)
Same as fromString, but without requiring the square brackets in the string.
bool isHorizontal(const double tolerance = 0) const
Return true if the 6D pose represents a Z axis almost exactly vertical (upwards or downwards), with a given tolerance (if set to 0 exact horizontality is tested).
double distanceEuclidean6D(const CPose3D& o) const
The euclidean distance between two poses taken as two 6-length vectors (angles in radians).
CPose3D getOppositeScalar() const
Return the opposite of the current pose instance by taking the negative of all its components individually.
virtual void setToNaN()
Set all data fields to quiet NaN.