Detailed Description
"lightweight" point & pose classes

|
Classes | |
| class | mrpt::math::CPolygon |
| A wrapper of a TPolygon2D class, implementing CSerializable. More... | |
| class | mrpt::math::TPolygonWithPlane |
| Slightly heavyweight type to speed-up calculations with polygons in 3D. More... | |
| struct | mrpt::math::TPoint2D |
| Lightweight 2D point. More... | |
| struct | mrpt::math::TPose2D |
| Lightweight 2D pose. More... | |
| struct | mrpt::math::TPoint3Df |
| Lightweight 3D point (float version). More... | |
| struct | mrpt::math::TPoint3D |
| Lightweight 3D point. More... | |
| struct | mrpt::math::TPointXYZIu8 |
| XYZ point (double) + Intensity(u8) More... | |
| struct | mrpt::math::TPointXYZRGBu8 |
| XYZ point (double) + RGB(u8) More... | |
| struct | mrpt::math::TPointXYZfIu8 |
| XYZ point (float) + Intensity(u8) More... | |
| struct | mrpt::math::TPointXYZfRGBu8 |
| XYZ point (float) + RGB(u8) More... | |
| struct | mrpt::math::TPose3D |
| Lightweight 3D pose (three spatial coordinates, plus three angular coordinates). More... | |
| struct | mrpt::math::TPose3DQuat |
| Lightweight 3D pose (three spatial coordinates, plus a quaternion ). More... | |
| struct | mrpt::math::TSegment2D |
| 2D segment, consisting of two points. More... | |
| struct | mrpt::math::TSegment3D |
| 3D segment, consisting of two points. More... | |
| struct | mrpt::math::TLine2D |
2D line without bounds, represented by its equation 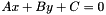 . More... . More... | |
| struct | mrpt::math::TLine3D |
| 3D line, represented by a base point and a director vector. More... | |
| struct | mrpt::math::TPlane |
3D Plane, represented by its equation 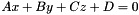 More... More... | |
| class | mrpt::math::TPolygon2D |
| 2D polygon, inheriting from std::vector<TPoint2D>. More... | |
| class | mrpt::math::TPolygon3D |
| 3D polygon, inheriting from std::vector<TPoint3D> More... | |
| struct | mrpt::math::TObject2D |
| Standard type for storing any lightweight 2D type. More... | |
| struct | mrpt::math::TObject3D |
| Standard object for storing any 3D lightweight object. More... | |
| struct | mrpt::math::TTwist2D |
| 2D twist: 2D velocity vector (vx,vy) + planar angular velocity (omega) More... | |
| struct | mrpt::math::TTwist3D |
| 3D twist: 3D velocity vector (vx,vy,vz) + angular velocity (wx,wy,wz) More... | |
Typedefs | |
| typedef TPlane | mrpt::math::TPlane3D |
Variables | |
| const unsigned char | mrpt::math::GEOMETRIC_TYPE_POINT = 0 |
| Object type identifier for TPoint2D or TPoint3D. More... | |
| const unsigned char | mrpt::math::GEOMETRIC_TYPE_SEGMENT = 1 |
| Object type identifier for TSegment2D or TSegment3D. More... | |
| const unsigned char | mrpt::math::GEOMETRIC_TYPE_LINE = 2 |
| Object type identifier for TLine2D or TLine3D. More... | |
| const unsigned char | mrpt::math::GEOMETRIC_TYPE_POLYGON = 3 |
| Object type identifier for TPolygon2D or TPolygon3D. More... | |
| const unsigned char | mrpt::math::GEOMETRIC_TYPE_PLANE = 4 |
| Object type identifier for TPlane. More... | |
| const unsigned char | mrpt::math::GEOMETRIC_TYPE_UNDEFINED = 255 |
| Object type identifier for empty TObject2D or TObject3D. More... | |
Simple intersection operations, relying basically on geometrical | |
| bool | mrpt::math::intersect (const TSegment3D &s1, const TSegment3D &s2, TObject3D &obj) |
| Gets the intersection between two 3D segments. More... | |
| bool | mrpt::math::intersect (const TSegment3D &s1, const TPlane &p2, TObject3D &obj) |
| Gets the intersection between a 3D segment and a plane. More... | |
| bool | mrpt::math::intersect (const TSegment3D &s1, const TLine3D &r2, TObject3D &obj) |
| Gets the intersection between a 3D segment and a 3D line. More... | |
| bool | mrpt::math::intersect (const TPlane &p1, const TSegment3D &s2, TObject3D &obj) |
| Gets the intersection between a plane and a 3D segment. More... | |
| bool | mrpt::math::intersect (const TPlane &p1, const TPlane &p2, TObject3D &obj) |
| Gets the intersection between two planes. More... | |
| bool | mrpt::math::intersect (const TPlane &p1, const TLine3D &p2, TObject3D &obj) |
| Gets the intersection between a plane and a 3D line. More... | |
| bool | mrpt::math::intersect (const TLine3D &r1, const TSegment3D &s2, TObject3D &obj) |
| Gets the intersection between a 3D line and a 3D segment. More... | |
| bool | mrpt::math::intersect (const TLine3D &r1, const TPlane &p2, TObject3D &obj) |
| Gets the intersection between a 3D line and a plane. More... | |
| bool | mrpt::math::intersect (const TLine3D &r1, const TLine3D &r2, TObject3D &obj) |
| Gets the intersection between two 3D lines. More... | |
| bool | mrpt::math::intersect (const TLine2D &r1, const TLine2D &r2, TObject2D &obj) |
| Gets the intersection between two 2D lines. More... | |
| bool | mrpt::math::intersect (const TLine2D &r1, const TSegment2D &s2, TObject2D &obj) |
| Gets the intersection between a 2D line and a 2D segment. More... | |
| bool | mrpt::math::intersect (const TSegment2D &s1, const TLine2D &r2, TObject2D &obj) |
| Gets the intersection between a 2D line and a 2D segment. More... | |
| bool | mrpt::math::intersect (const TSegment2D &s1, const TSegment2D &s2, TObject2D &obj) |
| Gets the intersection between two 2D segments. More... | |
Angle retrieval methods. Methods which use TSegments will | |
| double | mrpt::math::getAngle (const TPlane &p1, const TPlane &p2) |
| Computes the angle between two planes. More... | |
| double | mrpt::math::getAngle (const TPlane &p1, const TLine3D &r2) |
| Computes the angle between a plane and a 3D line or segment (implicit constructor will be used if passing a segment instead of a line). More... | |
| double | mrpt::math::getAngle (const TLine3D &r1, const TPlane &p2) |
| Computes the angle between a 3D line or segment and a plane (implicit constructor will be used if passing a segment instead of a line). More... | |
| double | mrpt::math::getAngle (const TLine3D &r1, const TLine3D &r2) |
| Computes the angle between two 3D lines or segments (implicit constructor will be used if passing a segment instead of a line). More... | |
| double | mrpt::math::getAngle (const TLine2D &r1, const TLine2D &r2) |
| Computes the angle between two 2D lines or segments (implicit constructor will be used if passing a segment instead of a line). More... | |
Creation of lines from poses. | |
| void | mrpt::math::createFromPoseX (const mrpt::poses::CPose3D &p, TLine3D &r) |
| Gets a 3D line corresponding to the X axis in a given pose. More... | |
| void | mrpt::math::createFromPoseY (const mrpt::poses::CPose3D &p, TLine3D &r) |
| Gets a 3D line corresponding to the Y axis in a given pose. More... | |
| void | mrpt::math::createFromPoseZ (const mrpt::poses::CPose3D &p, TLine3D &r) |
| Gets a 3D line corresponding to the Z axis in a given pose. More... | |
| void | mrpt::math::createFromPoseAndVector (const mrpt::poses::CPose3D &p, const double(&vector)[3], TLine3D &r) |
| Gets a 3D line corresponding to any arbitrary vector, in the base given by the pose. More... | |
| void | mrpt::math::createFromPoseX (const TPose2D &p, TLine2D &r) |
| Gets a 2D line corresponding to the X axis in a given pose. More... | |
| void | mrpt::math::createFromPoseY (const TPose2D &p, TLine2D &r) |
| Gets a 2D line corresponding to the Y axis in a given pose. More... | |
| void | mrpt::math::createFromPoseAndVector (const TPose2D &p, const double(&vector)[2], TLine2D &r) |
| Gets a 2D line corresponding to any arbitrary vector, in the base given the given pose. More... | |
Other line or plane related methods. | |
| bool | mrpt::math::conformAPlane (const std::vector< TPoint3D > &points) |
| Checks whether this polygon or set of points acceptably fits a plane. More... | |
| bool | mrpt::math::conformAPlane (const std::vector< TPoint3D > &points, TPlane &p) |
| Checks whether this polygon or set of points acceptably fits a plane, and if it's the case returns it in the second argument. More... | |
| bool | mrpt::math::areAligned (const std::vector< TPoint2D > &points) |
| Checks whether this set of points acceptably fits a 2D line. More... | |
| bool | mrpt::math::areAligned (const std::vector< TPoint2D > &points, TLine2D &r) |
| Checks whether this set of points acceptably fits a 2D line, and if it's the case returns it in the second argument. More... | |
| bool | mrpt::math::areAligned (const std::vector< TPoint3D > &points) |
| Checks whether this set of points acceptably fits a 3D line. More... | |
| bool | mrpt::math::areAligned (const std::vector< TPoint3D > &points, TLine3D &r) |
| Checks whether this set of points acceptably fits a 3D line, and if it's the case returns it in the second argument. More... | |
Projections | |
| void | mrpt::math::project3D (const TPoint3D &point, const mrpt::poses::CPose3D &newXYpose, TPoint3D &newPoint) |
| Uses the given pose 3D to project a point into a new base. More... | |
| void | mrpt::math::project3D (const TSegment3D &segment, const mrpt::poses::CPose3D &newXYpose, TSegment3D &newSegment) |
| Uses the given pose 3D to project a segment into a new base. More... | |
| void | mrpt::math::project3D (const TLine3D &line, const mrpt::poses::CPose3D &newXYpose, TLine3D &newLine) |
| Uses the given pose 3D to project a line into a new base. More... | |
| void | mrpt::math::project3D (const TPlane &plane, const mrpt::poses::CPose3D &newXYpose, TPlane &newPlane) |
| Uses the given pose 3D to project a plane into a new base. More... | |
| void | mrpt::math::project3D (const TPolygon3D &polygon, const mrpt::poses::CPose3D &newXYpose, TPolygon3D &newPolygon) |
| Uses the given pose 3D to project a polygon into a new base. More... | |
| void | mrpt::math::project3D (const TObject3D &object, const mrpt::poses::CPose3D &newXYPose, TObject3D &newObject) |
| Uses the given pose 3D to project any 3D object into a new base. More... | |
| template<class T > | |
| void | mrpt::math::project3D (const T &obj, const TPlane &newXYPlane, T &newObj) |
| Projects any 3D object into the plane's base, using its inverse pose. More... | |
| template<class T > | |
| void | mrpt::math::project3D (const T &obj, const TPlane &newXYPlane, const TPoint3D &newOrigin, T &newObj) |
| Projects any 3D object into the plane's base, using its inverse pose and forcing the position of the new coordinates origin. More... | |
| template<class T > | |
| void | mrpt::math::project3D (const std::vector< T > &objs, const mrpt::poses::CPose3D &newXYpose, std::vector< T > &newObjs) |
| Projects a set of 3D objects into the plane's base. More... | |
| void | mrpt::math::project2D (const TPoint2D &point, const mrpt::poses::CPose2D &newXpose, TPoint2D &newPoint) |
| Uses the given pose 2D to project a point into a new base. More... | |
| void | mrpt::math::project2D (const TSegment2D &segment, const mrpt::poses::CPose2D &newXpose, TSegment2D &newSegment) |
| Uses the given pose 2D to project a segment into a new base. More... | |
| void | mrpt::math::project2D (const TLine2D &line, const mrpt::poses::CPose2D &newXpose, TLine2D &newLine) |
| Uses the given pose 2D to project a line into a new base. More... | |
| void | mrpt::math::project2D (const TPolygon2D &polygon, const mrpt::poses::CPose2D &newXpose, TPolygon2D &newPolygon) |
| Uses the given pose 2D to project a polygon into a new base. More... | |
| void | mrpt::math::project2D (const TObject2D &object, const mrpt::poses::CPose2D &newXpose, TObject2D &newObject) |
| Uses the given pose 2D to project any 2D object into a new base. More... | |
| template<class T , class CPOSE2D > | |
| void | mrpt::math::project2D (const T &obj, const TLine2D &newXLine, T &newObj) |
| Projects any 2D object into the line's base, using its inverse pose. More... | |
| template<class T , class CPOSE2D > | |
| void | mrpt::math::project2D (const T &obj, const TLine2D &newXLine, const TPoint2D &newOrigin, T &newObj) |
| Projects any 2D object into the line's base, using its inverse pose and forcing the position of the new coordinate origin. More... | |
| template<class T > | |
| void | mrpt::math::project2D (const std::vector< T > &objs, const mrpt::poses::CPose2D &newXpose, std::vector< T > &newObjs) |
| Projects a set of 2D objects into the line's base. More... | |
Polygon intersections. These operations rely more on spatial reasoning | |
| bool | mrpt::math::intersect (const TPolygon2D &p1, const TSegment2D &s2, TObject2D &obj) |
| Gets the intersection between a 2D polygon and a 2D segment. More... | |
| bool | mrpt::math::intersect (const TPolygon2D &p1, const TLine2D &r2, TObject2D &obj) |
| Gets the intersection between a 2D polygon and a 2D line. More... | |
| bool | mrpt::math::intersect (const TPolygon2D &p1, const TPolygon2D &p2, TObject2D &obj) |
| Gets the intersection between two 2D polygons. More... | |
| bool | mrpt::math::intersect (const TSegment2D &s1, const TPolygon2D &p2, TObject2D &obj) |
| Gets the intersection between a 2D segment and a 2D polygon. More... | |
| bool | mrpt::math::intersect (const TLine2D &r1, const TPolygon2D &p2, TObject2D &obj) |
| Gets the intersection between a 2D line and a 2D polygon. More... | |
| bool | mrpt::math::intersect (const TPolygon3D &p1, const TSegment3D &s2, TObject3D &obj) |
| Gets the intersection between a 3D polygon and a 3D segment. More... | |
| bool | mrpt::math::intersect (const TPolygon3D &p1, const TLine3D &r2, TObject3D &obj) |
| Gets the intersection between a 3D polygon and a 3D line. More... | |
| bool | mrpt::math::intersect (const TPolygon3D &p1, const TPlane &p2, TObject3D &obj) |
| Gets the intersection between a 3D polygon and a plane. More... | |
| bool | mrpt::math::intersect (const TPolygon3D &p1, const TPolygon3D &p2, TObject3D &obj) |
| Gets the intersection between two 3D polygons. More... | |
| bool | mrpt::math::intersect (const TSegment3D &s1, const TPolygon3D &p2, TObject3D &obj) |
| Gets the intersection between a 3D segment and a 3D polygon. More... | |
| bool | mrpt::math::intersect (const TLine3D &r1, const TPolygon3D &p2, TObject3D &obj) |
| Gets the intersection between a 3D line and a 3D polygon. More... | |
| bool | mrpt::math::intersect (const TPlane &p1, const TPolygon3D &p2, TObject3D &obj) |
| Gets the intersection between a plane and a 3D polygon. More... | |
| size_t | mrpt::math::intersect (const std::vector< TPolygon3D > &v1, const std::vector< TPolygon3D > &v2, CSparseMatrixTemplate< TObject3D > &objs) |
| Gets the intersection between two sets of 3D polygons. More... | |
| size_t | mrpt::math::intersect (const std::vector< TPolygon3D > &v1, const std::vector< TPolygon3D > &v2, std::vector< TObject3D > &objs) |
| Gets the intersection between two sets of 3D polygons. More... | |
Other intersections | |
| template<class T , class U , class O > | |
| size_t | mrpt::math::intersect (const std::vector< T > &v1, const std::vector< U > &v2, CSparseMatrixTemplate< O > &objs) |
| Gets the intersection between vectors of geometric objects and returns it in a sparse matrix of either TObject2D or TObject3D. More... | |
| template<class T , class U , class O > | |
| size_t | mrpt::math::intersect (const std::vector< T > &v1, const std::vector< U > &v2, std::vector< O > objs) |
| Gets the intersection between vectors of geometric objects and returns it in a vector of either TObject2D or TObject3D. More... | |
| bool | mrpt::math::intersect (const TObject2D &o1, const TObject2D &o2, TObject2D &obj) |
| Gets the intersection between any pair of 2D objects. More... | |
| bool | mrpt::math::intersect (const TObject3D &o1, const TObject3D &o2, TObject3D &obj) |
| Gets the intersection between any pair of 3D objects. More... | |
Distances | |
| double | mrpt::math::distance (const TPoint2D &p1, const TPoint2D &p2) |
| Gets the distance between two points in a 2D space. More... | |
| double | mrpt::math::distance (const TPoint3D &p1, const TPoint3D &p2) |
| Gets the distance between two points in a 3D space. More... | |
| double | mrpt::math::distance (const TLine2D &r1, const TLine2D &r2) |
| Gets the distance between two lines in a 2D space. More... | |
| double | mrpt::math::distance (const TLine3D &r1, const TLine3D &r2) |
| Gets the distance between two lines in a 3D space. More... | |
| double | mrpt::math::distance (const TPlane &p1, const TPlane &p2) |
| Gets the distance between two planes. More... | |
| double | mrpt::math::distance (const TPolygon2D &p1, const TPolygon2D &p2) |
| Gets the distance between two polygons in a 2D space. More... | |
| double | mrpt::math::distance (const TPolygon2D &p1, const TSegment2D &s2) |
| Gets the distance between a polygon and a segment in a 2D space. More... | |
| double | mrpt::math::distance (const TSegment2D &s1, const TPolygon2D &p2) |
| Gets the distance between a segment and a polygon in a 2D space. More... | |
| double | mrpt::math::distance (const TPolygon2D &p1, const TLine2D &l2) |
| Gets the distance between a polygon and a line in a 2D space. More... | |
| double | mrpt::math::distance (const TLine2D &l1, const TPolygon2D &p2) |
| double | mrpt::math::distance (const TPolygon3D &p1, const TPolygon3D &p2) |
| Gets the distance between two polygons in a 3D space. More... | |
| double | mrpt::math::distance (const TPolygon3D &p1, const TSegment3D &s2) |
| Gets the distance between a polygon and a segment in a 3D space. More... | |
| double | mrpt::math::distance (const TSegment3D &s1, const TPolygon3D &p2) |
| Gets the distance between a segment and a polygon in a 3D space. More... | |
| double | mrpt::math::distance (const TPolygon3D &p1, const TLine3D &l2) |
| Gets the distance between a polygon and a line in a 3D space. More... | |
| double | mrpt::math::distance (const TLine3D &l1, const TPolygon3D &p2) |
| Gets the distance between a line and a polygon in a 3D space. More... | |
| double | mrpt::math::distance (const TPolygon3D &po, const TPlane &pl) |
| Gets the distance between a polygon and a plane. More... | |
| double | mrpt::math::distance (const TPlane &pl, const TPolygon3D &po) |
| Gets the distance between a plane and a polygon. More... | |
Bound checkers | |
| void | mrpt::math::getRectangleBounds (const std::vector< TPoint2D > &poly, TPoint2D &pMin, TPoint2D &pMax) |
| Gets the rectangular bounds of a 2D polygon or set of 2D points. More... | |
| void | mrpt::math::getPrismBounds (const std::vector< TPoint3D > &poly, TPoint3D &pMin, TPoint3D &pMax) |
| Gets the prism bounds of a 3D polygon or set of 3D points. More... | |
Creation of planes from poses | |
| void | mrpt::math::createPlaneFromPoseXY (const mrpt::poses::CPose3D &pose, TPlane &plane) |
| Given a pose, creates a plane orthogonal to its Z vector. More... | |
| void | mrpt::math::createPlaneFromPoseXZ (const mrpt::poses::CPose3D &pose, TPlane &plane) |
| Given a pose, creates a plane orthogonal to its Y vector. More... | |
| void | mrpt::math::createPlaneFromPoseYZ (const mrpt::poses::CPose3D &pose, TPlane &plane) |
| Given a pose, creates a plane orthogonal to its X vector. More... | |
| void | mrpt::math::createPlaneFromPoseAndNormal (const mrpt::poses::CPose3D &pose, const double(&normal)[3], TPlane &plane) |
| Given a pose and any vector, creates a plane orthogonal to that vector in the pose's coordinates. More... | |
| void | mrpt::math::generateAxisBaseFromDirectionAndAxis (const double(&vec)[3], char coord, CMatrixDouble &matrix) |
| Creates a homogeneus matrix (4x4) such that the coordinate given (0 for x, 1 for y, 2 for z) corresponds to the provided vector. More... | |
Linear regression methods | |
| double | mrpt::math::getRegressionLine (const std::vector< TPoint2D > &points, TLine2D &line) |
| Using eigenvalues, gets the best fitting line for a set of 2D points. More... | |
| double | mrpt::math::getRegressionLine (const std::vector< TPoint3D > &points, TLine3D &line) |
| Using eigenvalues, gets the best fitting line for a set of 3D points. More... | |
| double | mrpt::math::getRegressionPlane (const std::vector< TPoint3D > &points, TPlane &plane) |
| Using eigenvalues, gets the best fitting plane for a set of 3D points. More... | |
Miscellaneous Geometry methods | |
| void | mrpt::math::assemblePolygons (const std::vector< TSegment3D > &segms, std::vector< TPolygon3D > &polys) |
| Tries to assemble a set of segments into a set of closed polygons. More... | |
| void | mrpt::math::assemblePolygons (const std::vector< TSegment3D > &segms, std::vector< TPolygon3D > &polys, std::vector< TSegment3D > &remainder) |
| Tries to assemble a set of segments into a set of closed polygons, returning the unused segments as another out parameter. More... | |
| void | mrpt::math::assemblePolygons (const std::vector< TObject3D > &objs, std::vector< TPolygon3D > &polys) |
| Extracts all the polygons, including those formed from segments, from the set of objects. More... | |
| void | mrpt::math::assemblePolygons (const std::vector< TObject3D > &objs, std::vector< TPolygon3D > &polys, std::vector< TObject3D > &remainder) |
| Extracts all the polygons, including those formed from segments, from the set of objects. More... | |
| void | mrpt::math::assemblePolygons (const std::vector< TObject3D > &objs, std::vector< TPolygon3D > &polys, std::vector< TSegment3D > &remainder1, std::vector< TObject3D > &remainder2) |
| Extracts all the polygons, including those formed from segments, from the set of objects. More... | |
| void | mrpt::math::setEpsilon (double nE) |
| Changes the value of the geometric epsilon (default = 1e-5) More... | |
| double | mrpt::math::getEpsilon () |
| Gets the value of the geometric epsilon (default = 1e-5) More... | |
| bool | mrpt::math::splitInConvexComponents (const TPolygon2D &poly, std::vector< TPolygon2D > &components) |
| Splits a 2D polygon into convex components. More... | |
| bool | mrpt::math::splitInConvexComponents (const TPolygon3D &poly, std::vector< TPolygon3D > &components) |
| Splits a 3D polygon into convex components. More... | |
| void | mrpt::math::getSegmentBisector (const TSegment2D &sgm, TLine2D &bis) |
| Gets the bisector of a 2D segment. More... | |
| void | mrpt::math::getSegmentBisector (const TSegment3D &sgm, TPlane &bis) |
| Gets the bisector of a 3D segment. More... | |
| void | mrpt::math::getAngleBisector (const TLine2D &l1, const TLine2D &l2, TLine2D &bis) |
| Gets the bisector of two lines or segments (implicit constructor will be used if necessary) More... | |
| void | mrpt::math::getAngleBisector (const TLine3D &l1, const TLine3D &l2, TLine3D &bis) |
| Gets the bisector of two lines or segments (implicit constructor will be used if necessary) More... | |
| bool | mrpt::math::traceRay (const std::vector< TPolygonWithPlane > &vec, const mrpt::poses::CPose3D &pose, double &dist) |
| Fast ray tracing method using polygons' properties. More... | |
| bool | mrpt::math::traceRay (const std::vector< TPolygon3D > &vec, const mrpt::poses::CPose3D &pose, double &dist) |
| Fast ray tracing method using polygons' properties. More... | |
| template<class T , class U , class V > | |
| void | mrpt::math::crossProduct3D (const T &v0, const U &v1, V &vOut) |
| Computes the cross product of two 3D vectors, returning a vector normal to both. More... | |
| template<class T > | |
| void | mrpt::math::crossProduct3D (const std::vector< T > &v0, const std::vector< T > &v1, std::vector< T > &v_out) |
| template<class VEC1 , class VEC2 > | |
| Eigen::Matrix< double, 3, 1 > | mrpt::math::crossProduct3D (const VEC1 &v0, const VEC2 &v1) |
| overload (returning a vector of size 3 by value). More... | |
| template<class VECTOR , class MATRIX > | |
| void | mrpt::math::skew_symmetric3 (const VECTOR &v, MATRIX &M) |
| Computes the 3x3 skew symmetric matrix from a 3-vector or 3-array:
. More... | |
| template<class VECTOR > | |
| mrpt::math::CMatrixDouble33 | mrpt::math::skew_symmetric3 (const VECTOR &v) |
| template<class VECTOR , class MATRIX > | |
| void | mrpt::math::skew_symmetric3_neg (const VECTOR &v, MATRIX &M) |
| Computes the negative version of a 3x3 skew symmetric matrix from a 3-vector or 3-array:
. More... | |
| template<class VECTOR > | |
| mrpt::math::CMatrixDouble33 | mrpt::math::skew_symmetric3_neg (const VECTOR &v) |
| template<class T , class U > | |
| bool | mrpt::math::vectorsAreParallel2D (const T &v1, const U &v2) |
| Returns true if two 2D vectors are parallel. More... | |
| template<class T , class U > | |
| bool | mrpt::math::vectorsAreParallel3D (const T &v1, const U &v2) |
| Returns true if two 3D vectors are parallel. More... | |
| void | mrpt::math::closestFromPointToSegment (const double &Px, const double &Py, const double &x1, const double &y1, const double &x2, const double &y2, double &out_x, double &out_y) |
| Computes the closest point from a given point to a segment. More... | |
| void | mrpt::math::closestFromPointToLine (const double &Px, const double &Py, const double &x1, const double &y1, const double &x2, const double &y2, double &out_x, double &out_y) |
| Computes the closest point from a given point to a (infinite) line. More... | |
| double | mrpt::math::closestSquareDistanceFromPointToLine (const double &Px, const double &Py, const double &x1, const double &y1, const double &x2, const double &y2) |
| Returns the square distance from a point to a line. More... | |
| template<typename T > | |
| T | mrpt::math::distanceBetweenPoints (const T x1, const T y1, const T x2, const T y2) |
| Returns the distance between 2 points in 2D. More... | |
| template<typename T > | |
| T | mrpt::math::distanceBetweenPoints (const T x1, const T y1, const T z1, const T x2, const T y2, const T z2) |
| Returns the distance between 2 points in 3D. More... | |
| template<typename T > | |
| T | mrpt::math::distanceSqrBetweenPoints (const T x1, const T y1, const T x2, const T y2) |
| Returns the square distance between 2 points in 2D. More... | |
| template<typename T > | |
| T | mrpt::math::distanceSqrBetweenPoints (const T x1, const T y1, const T z1, const T x2, const T y2, const T z2) |
| Returns the square distance between 2 points in 3D. More... | |
| template<typename T > | |
| double | mrpt::math::minimumDistanceFromPointToSegment (const double Px, const double Py, const double x1, const double y1, const double x2, const double y2, T &out_x, T &out_y) |
| Computes the closest point from a given point to a segment, and returns that minimum distance. More... | |
| bool | mrpt::math::SegmentsIntersection (const double x1, const double y1, const double x2, const double y2, const double x3, const double y3, const double x4, const double y4, double &ix, double &iy) |
| Returns the intersection point, and if it exists, between two segments. More... | |
| bool | mrpt::math::SegmentsIntersection (const double x1, const double y1, const double x2, const double y2, const double x3, const double y3, const double x4, const double y4, float &ix, float &iy) |
| Returns the intersection point, and if it exists, between two segments. More... | |
| bool | mrpt::math::pointIntoPolygon2D (const double &px, const double &py, unsigned int polyEdges, const double *poly_xs, const double *poly_ys) |
| Returns true if the 2D point (px,py) falls INTO the given polygon. More... | |
| template<typename T > | |
| bool | mrpt::math::pointIntoQuadrangle (T x, T y, T v1x, T v1y, T v2x, T v2y, T v3x, T v3y, T v4x, T v4y) |
| Specialized method to check whether a point (x,y) falls into a quadrangle. More... | |
| double | mrpt::math::distancePointToPolygon2D (const double &px, const double &py, unsigned int polyEdges, const double *poly_xs, const double *poly_ys) |
| Returns the closest distance of a given 2D point to a polygon, or "0" if the point is INTO the polygon or its perimeter. More... | |
| bool | mrpt::math::minDistBetweenLines (const double &p1_x, const double &p1_y, const double &p1_z, const double &p2_x, const double &p2_y, const double &p2_z, const double &p3_x, const double &p3_y, const double &p3_z, const double &p4_x, const double &p4_y, const double &p4_z, double &x, double &y, double &z, double &dist) |
| Calculates the minimum distance between a pair of lines. More... | |
| bool | mrpt::math::RectanglesIntersection (const double &R1_x_min, const double &R1_x_max, const double &R1_y_min, const double &R1_y_max, const double &R2_x_min, const double &R2_x_max, const double &R2_y_min, const double &R2_y_max, const double &R2_pose_x, const double &R2_pose_y, const double &R2_pose_phi) |
| Returns whether two rotated rectangles intersect. More... | |
| template<class T > | |
| CMatrixTemplateNumeric< T > | mrpt::math::generateAxisBaseFromDirection (T dx, T dy, T dz) |
| Computes an axis base (a set of three 3D normal vectors) with the given vector being the first of them ("X") NOTE: Make sure of passing all floats or doubles and that the template of the receiving matrix is of the same type! More... | |
SLERP (Spherical Linear Interpolation) functions | |
| template<typename T > | |
| void | mrpt::math::slerp (const CQuaternion< T > &q0, const CQuaternion< T > &q1, const double t, CQuaternion< T > &q) |
| SLERP interpolation between two quaternions. More... | |
| void | mrpt::math::slerp (const mrpt::poses::CPose3D &q0, const mrpt::poses::CPose3D &q1, const double t, mrpt::poses::CPose3D &p) |
| SLERP interpolation between two 6D poses - like mrpt::math::slerp for quaternions, but interpolates the [X,Y,Z] coordinates as well. More... | |
| void | mrpt::math::slerp (const mrpt::poses::CPose3DQuat &q0, const mrpt::poses::CPose3DQuat &q1, const double t, mrpt::poses::CPose3DQuat &p) |
| void | mrpt::math::slerp_ypr (const mrpt::math::TPose3D &q0, const mrpt::math::TPose3D &q1, const double t, mrpt::math::TPose3D &p) |
Typedef Documentation
◆ TPlane3D
| typedef TPlane mrpt::math::TPlane3D |
Definition at line 1445 of file lightweight_geom_data.h.
Function Documentation
◆ areAligned() [1/4]
| bool mrpt::math::areAligned | ( | const std::vector< TPoint2D > & | points | ) |
Checks whether this set of points acceptably fits a 2D line.
- See also
- getEpsilon
Definition at line 1016 of file geometry.cpp.
References geometryEpsilon, mrpt::math::TPoint2D::x, and mrpt::math::TPoint2D::y.
Referenced by mrpt::math::areAligned().

◆ areAligned() [2/4]
Checks whether this set of points acceptably fits a 2D line, and if it's the case returns it in the second argument.
- See also
- getEpsilon
Definition at line 1031 of file geometry.cpp.
References mrpt::math::areAligned().

◆ areAligned() [3/4]
| bool mrpt::math::areAligned | ( | const std::vector< TPoint3D > & | points | ) |
Checks whether this set of points acceptably fits a 3D line.
- See also
- getEpsilon
Definition at line 1045 of file geometry.cpp.
References geometryEpsilon, mrpt::math::TPoint3D::x, mrpt::math::TPoint3D::y, and mrpt::math::TPoint3D::z.
◆ areAligned() [4/4]
Checks whether this set of points acceptably fits a 3D line, and if it's the case returns it in the second argument.
Definition at line 1061 of file geometry.cpp.
References mrpt::math::areAligned().

◆ assemblePolygons() [1/5]
| void mrpt::math::assemblePolygons | ( | const std::vector< TSegment3D > & | segms, |
| std::vector< TPolygon3D > & | polys | ||
| ) |
Tries to assemble a set of segments into a set of closed polygons.
Definition at line 2183 of file geometry.cpp.
Referenced by mrpt::math::assemblePolygons().

◆ assemblePolygons() [2/5]
| void mrpt::math::assemblePolygons | ( | const std::vector< TSegment3D > & | segms, |
| std::vector< TPolygon3D > & | polys, | ||
| std::vector< TSegment3D > & | remainder | ||
| ) |
Tries to assemble a set of segments into a set of closed polygons, returning the unused segments as another out parameter.
Definition at line 2281 of file geometry.cpp.
References depthFirstSearch(), mrpt::math::distance(), and geometryEpsilon.
◆ assemblePolygons() [3/5]
| void mrpt::math::assemblePolygons | ( | const std::vector< TObject3D > & | objs, |
| std::vector< TPolygon3D > & | polys | ||
| ) |
Extracts all the polygons, including those formed from segments, from the set of objects.
Definition at line 2329 of file geometry.cpp.
References mrpt::math::assemblePolygons(), mrpt::math::TObject3D::getPolygons(), and mrpt::math::TObject3D::getSegments().

◆ assemblePolygons() [4/5]
| void mrpt::math::assemblePolygons | ( | const std::vector< TObject3D > & | objs, |
| std::vector< TPolygon3D > & | polys, | ||
| std::vector< TObject3D > & | remainder | ||
| ) |
Extracts all the polygons, including those formed from segments, from the set of objects.
Definition at line 2339 of file geometry.cpp.
References mrpt::math::assemblePolygons(), mrpt::math::TObject3D::getPolygons(), and mrpt::math::TObject3D::getSegments().

◆ assemblePolygons() [5/5]
| void mrpt::math::assemblePolygons | ( | const std::vector< TObject3D > & | objs, |
| std::vector< TPolygon3D > & | polys, | ||
| std::vector< TSegment3D > & | remainder1, | ||
| std::vector< TObject3D > & | remainder2 | ||
| ) |
Extracts all the polygons, including those formed from segments, from the set of objects.
Definition at line 2352 of file geometry.cpp.
References mrpt::math::assemblePolygons(), mrpt::math::TObject3D::getPolygons(), and mrpt::math::TObject3D::getSegments().
◆ closestFromPointToLine()
| void mrpt::math::closestFromPointToLine | ( | const double & | Px, |
| const double & | Py, | ||
| const double & | x1, | ||
| const double & | y1, | ||
| const double & | x2, | ||
| const double & | y2, | ||
| double & | out_x, | ||
| double & | out_y | ||
| ) |
Computes the closest point from a given point to a (infinite) line.
- See also
- closestFromPointToSegment
Definition at line 80 of file geometry.cpp.
Referenced by mrpt::maps::CPointsMap::squareDistanceToClosestCorrespondence().

◆ closestFromPointToSegment()
| void mrpt::math::closestFromPointToSegment | ( | const double & | Px, |
| const double & | Py, | ||
| const double & | x1, | ||
| const double & | y1, | ||
| const double & | x2, | ||
| const double & | y2, | ||
| double & | out_x, | ||
| double & | out_y | ||
| ) |
Computes the closest point from a given point to a segment.
- See also
- closestFromPointToLine
Definition at line 42 of file geometry.cpp.
◆ closestSquareDistanceFromPointToLine()
| double mrpt::math::closestSquareDistanceFromPointToLine | ( | const double & | Px, |
| const double & | Py, | ||
| const double & | x1, | ||
| const double & | y1, | ||
| const double & | x2, | ||
| const double & | y2 | ||
| ) |
Returns the square distance from a point to a line.
Definition at line 103 of file geometry.cpp.
References mrpt::math::square().
Referenced by mrpt::slam::CICP::ICP_Method_LM().


◆ conformAPlane() [1/2]
| bool mrpt::math::conformAPlane | ( | const std::vector< TPoint3D > & | points | ) |
Checks whether this polygon or set of points acceptably fits a plane.
- See also
- TPolygon3D,getEpsilon
Definition at line 995 of file geometry.cpp.
References geometryEpsilon, mrpt::math::TPoint3D::x, mrpt::math::TPoint3D::y, and mrpt::math::TPoint3D::z.
Referenced by mrpt::math::TPolygon3D::getPlane(), and mrpt::math::TPolygon3D::isSkew().

◆ conformAPlane() [2/2]
Checks whether this polygon or set of points acceptably fits a plane, and if it's the case returns it in the second argument.
- See also
- TPolygon3D,getEpsilon
Definition at line 1011 of file geometry.cpp.
References geometryEpsilon, and mrpt::math::getRegressionPlane().

◆ createFromPoseAndVector() [1/2]
| void mrpt::math::createFromPoseAndVector | ( | const mrpt::poses::CPose3D & | p, |
| const double(&) | vector[3], | ||
| TLine3D & | r | ||
| ) |
Gets a 3D line corresponding to any arbitrary vector, in the base given by the pose.
An implicit constructor is used if a TPose3D is given.
Definition at line 958 of file geometry.cpp.
◆ createFromPoseAndVector() [2/2]
| void mrpt::math::createFromPoseAndVector | ( | const TPose2D & | p, |
| const double(&) | vector[2], | ||
| TLine2D & | r | ||
| ) |
Gets a 2D line corresponding to any arbitrary vector, in the base given the given pose.
An implicit constructor is used if a CPose2D is given.
Definition at line 985 of file geometry.cpp.
◆ createFromPoseX() [1/2]
| void mrpt::math::createFromPoseX | ( | const mrpt::poses::CPose3D & | p, |
| TLine3D & | r | ||
| ) |
Gets a 3D line corresponding to the X axis in a given pose.
An implicit constructor is used if a TPose3D is given.
Definition at line 943 of file geometry.cpp.
References createFromPoseAndAxis().
Referenced by mrpt::opengl::CCylinder::traceRay(), mrpt::opengl::CEllipsoid::traceRay(), and mrpt::math::traceRay().

◆ createFromPoseX() [2/2]
Gets a 2D line corresponding to the X axis in a given pose.
An implicit constructor is used if a CPose2D is given.
Definition at line 971 of file geometry.cpp.
◆ createFromPoseY() [1/2]
| void mrpt::math::createFromPoseY | ( | const mrpt::poses::CPose3D & | p, |
| TLine3D & | r | ||
| ) |
Gets a 3D line corresponding to the Y axis in a given pose.
An implicit constructor is used if a TPose3D is given.
Definition at line 948 of file geometry.cpp.
References createFromPoseAndAxis().

◆ createFromPoseY() [2/2]
Gets a 2D line corresponding to the Y axis in a given pose.
An implicit constructor is used if a CPose2D is given.
Definition at line 978 of file geometry.cpp.
◆ createFromPoseZ()
| void mrpt::math::createFromPoseZ | ( | const mrpt::poses::CPose3D & | p, |
| TLine3D & | r | ||
| ) |
Gets a 3D line corresponding to the Z axis in a given pose.
An implicit constructor is used if a TPose3D is given.
Definition at line 953 of file geometry.cpp.
References createFromPoseAndAxis().

◆ createPlaneFromPoseAndNormal()
| void mrpt::math::createPlaneFromPoseAndNormal | ( | const mrpt::poses::CPose3D & | pose, |
| const double(&) | normal[3], | ||
| TPlane & | plane | ||
| ) |
Given a pose and any vector, creates a plane orthogonal to that vector in the pose's coordinates.
Definition at line 2059 of file geometry.cpp.
References mrpt::math::TPlane::coefs, and mrpt::poses::CPose3D::getHomogeneousMatrixVal().

◆ createPlaneFromPoseXY()
| void mrpt::math::createPlaneFromPoseXY | ( | const mrpt::poses::CPose3D & | pose, |
| TPlane & | plane | ||
| ) |
Given a pose, creates a plane orthogonal to its Z vector.
Definition at line 2044 of file geometry.cpp.
References createPlaneFromPoseAndAxis().

◆ createPlaneFromPoseXZ()
| void mrpt::math::createPlaneFromPoseXZ | ( | const mrpt::poses::CPose3D & | pose, |
| TPlane & | plane | ||
| ) |
Given a pose, creates a plane orthogonal to its Y vector.
Definition at line 2049 of file geometry.cpp.
References createPlaneFromPoseAndAxis().

◆ createPlaneFromPoseYZ()
| void mrpt::math::createPlaneFromPoseYZ | ( | const mrpt::poses::CPose3D & | pose, |
| TPlane & | plane | ||
| ) |
Given a pose, creates a plane orthogonal to its X vector.
Definition at line 2054 of file geometry.cpp.
References createPlaneFromPoseAndAxis().

◆ crossProduct3D() [1/3]
|
inline |
Computes the cross product of two 3D vectors, returning a vector normal to both.
It uses the simple implementation:
![\[ v_out = \left( \begin{array}{c c c} \hat{i} ~ \hat{j} ~ \hat{k} \\ x0 ~ y0 ~ z0 \\ x1 ~ y1 ~ z1 \\ \end{array} \right) \]](form_28.png)
Definition at line 811 of file geometry.h.
Referenced by mrpt::math::distance(), mrpt::topography::ENUToGeocentric(), mrpt::vision::findMultipleChessboardsCorners(), mrpt::math::generateAxisBaseFromDirection(), mrpt::opengl::COpenGLViewport::get3DRayForPixelCoord(), mrpt::math::intersect(), mrpt::opengl::CArrow::render_dl(), and mrpt::math::TPlane::TPlane().
◆ crossProduct3D() [2/3]
|
inline |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
Definition at line 820 of file geometry.h.
◆ crossProduct3D() [3/3]
|
inline |
overload (returning a vector of size 3 by value).
Definition at line 833 of file geometry.h.
References ASSERT_.
◆ distance() [1/17]
Gets the distance between two points in a 2D space.
Definition at line 1885 of file geometry.cpp.
References mrpt::math::TPoint2D::x, and mrpt::math::TPoint2D::y.
Referenced by mrpt::math::assemblePolygons(), mrpt::detectors::CFaceDetection::checkIfDiagonalSurface(), mrpt::detectors::CFaceDetection::checkIfDiagonalSurface2(), mrpt::maps::CPointsMap::compute3DDistanceToMesh(), mrpt::math::confidenceIntervals(), mrpt::math::TSegment2D::contains(), mrpt::math::TSegment3D::contains(), mrpt::hwdrivers::CIbeoLuxETH::convertToCartesian(), mrpt::vision::CFeature::descriptorORBDistanceTo(), mrpt::math::distance(), mrpt::math::TSegment3D::distance(), mrpt::poses::CPoseInterpolatorBase< 3 >::filter(), find_chessboard_corners_multiple(), mrpt::utils::find_in_vector(), mrpt::obs::CRawlog::findObservationsByClassInRange(), getHeight(), mrpt::graphslam::deciders::CICPCriteriaERD< GRAPH_T >::getNearbyNodesOf(), mrpt::graphslam::optimizers::CLevMarqGSO< GRAPH_T >::getNearbyNodesOf(), mrpt::poses::CPoseInterpolatorBase< 3 >::getPreviousPoseWithMinDistance(), mrpt::math::CBinaryRelation< T, U, UIsObject >::getRelationFrom(), mrpt::math::CBinaryRelation< T, U, UIsObject >::getRelationTo(), mrpt::math::CBinaryRelation< T, U, UIsObject >::getRelationValue(), mrpt::math::CBinaryRelation< T, U, UIsObject >::insertElement(), mrpt::math::CBinaryRelation< T, U, UIsObject >::insertElements(), mrpt::maps::CLandmarksMap::internal_computeObservationLikelihood(), mrpt::math::intersect(), mrpt::opengl::CPolyhedron::TPolyhedronEdge::length(), mrpt::math::TSegment2D::length(), mrpt::math::TSegment3D::length(), mrpt::slam::AuxiliaryPFStandardAndOptimal< USE_OPTIMAL_SAMPLING >::PF_SLAM_implementation(), mrpt::math::CBinaryRelation< T, U, UIsObject >::removeElement(), mrpt::math::CBinaryRelation< T, U, UIsObject >::removeElements(), mrpt::math::removeRepVertices(), mrpt::math::removeUnusedVertices(), mrpt::bayes::CKalmanFilterCapable< 7, 3, 3, 7 >::runOneKalmanIteration(), mrpt::math::CBinaryRelation< T, U, UIsObject >::setRelationValue(), mrpt::math::TSegment2D::signedDistance(), mrpt::math::splitInConvexComponents(), mrpt::math::TLine3D::TLine3D(), and velodyne_scan_to_pointcloud().
◆ distance() [2/17]
Gets the distance between two points in a 3D space.
Definition at line 1892 of file geometry.cpp.
References mrpt::math::TPoint3D::x, mrpt::math::TPoint3D::y, and mrpt::math::TPoint3D::z.
◆ distance() [3/17]
Gets the distance between two lines in a 2D space.
Definition at line 1916 of file geometry.cpp.
References mrpt::math::TLine2D::coefs, mrpt::math::TLine2D::distance(), and geometryEpsilon.

◆ distance() [4/17]
Gets the distance between two lines in a 3D space.
Definition at line 1932 of file geometry.cpp.
References mrpt::math::crossProduct3D(), mrpt::math::TLine3D::director, mrpt::math::TLine3D::distance(), geometryEpsilon, mrpt::math::getAngle(), and mrpt::math::TLine3D::pBase.

◆ distance() [5/17]
Gets the distance between two planes.
It will be zero if the planes are not parallel.
Definition at line 1948 of file geometry.cpp.
References mrpt::math::TPlane::coefs, mrpt::math::TPlane::distance(), geometryEpsilon, and mrpt::math::getAngle().

◆ distance() [6/17]
| double mrpt::math::distance | ( | const TPolygon2D & | p1, |
| const TPolygon2D & | p2 | ||
| ) |
Gets the distance between two polygons in a 2D space.
Definition at line 1966 of file geometry.cpp.
References MRPT_UNUSED_PARAM, and THROW_EXCEPTION.
◆ distance() [7/17]
| double mrpt::math::distance | ( | const TPolygon2D & | p1, |
| const TSegment2D & | s2 | ||
| ) |
Gets the distance between a polygon and a segment in a 2D space.
Definition at line 1973 of file geometry.cpp.
References MRPT_UNUSED_PARAM, and THROW_EXCEPTION.
◆ distance() [8/17]
|
inline |
Gets the distance between a segment and a polygon in a 2D space.
Definition at line 596 of file geometry.h.
◆ distance() [9/17]
| double mrpt::math::distance | ( | const TPolygon2D & | p1, |
| const TLine2D & | l2 | ||
| ) |
Gets the distance between a polygon and a line in a 2D space.
Definition at line 1980 of file geometry.cpp.
References MRPT_UNUSED_PARAM, and THROW_EXCEPTION.
◆ distance() [10/17]
|
inline |
Definition at line 602 of file geometry.h.
References mrpt::math::distance().

◆ distance() [11/17]
| double mrpt::math::distance | ( | const TPolygon3D & | p1, |
| const TPolygon3D & | p2 | ||
| ) |
Gets the distance between two polygons in a 3D space.
Definition at line 1987 of file geometry.cpp.
References MRPT_UNUSED_PARAM, and THROW_EXCEPTION.
◆ distance() [12/17]
| double mrpt::math::distance | ( | const TPolygon3D & | p1, |
| const TSegment3D & | s2 | ||
| ) |
Gets the distance between a polygon and a segment in a 3D space.
Definition at line 1994 of file geometry.cpp.
References MRPT_UNUSED_PARAM, and THROW_EXCEPTION.
◆ distance() [13/17]
|
inline |
Gets the distance between a segment and a polygon in a 3D space.
Definition at line 611 of file geometry.h.
◆ distance() [14/17]
| double mrpt::math::distance | ( | const TPolygon3D & | p1, |
| const TLine3D & | l2 | ||
| ) |
Gets the distance between a polygon and a line in a 3D space.
Definition at line 2001 of file geometry.cpp.
References MRPT_UNUSED_PARAM, and THROW_EXCEPTION.
◆ distance() [15/17]
|
inline |
Gets the distance between a line and a polygon in a 3D space.
Definition at line 618 of file geometry.h.
References mrpt::math::distance().

◆ distance() [16/17]
| double mrpt::math::distance | ( | const TPolygon3D & | po, |
| const TPlane & | pl | ||
| ) |
Gets the distance between a polygon and a plane.
Definition at line 2008 of file geometry.cpp.
References MRPT_UNUSED_PARAM, and THROW_EXCEPTION.
◆ distance() [17/17]
|
inline |
Gets the distance between a plane and a polygon.
Definition at line 625 of file geometry.h.
References mrpt::math::distance().

◆ distanceBetweenPoints() [1/2]
| T mrpt::math::distanceBetweenPoints | ( | const T | x1, |
| const T | y1, | ||
| const T | x2, | ||
| const T | y2 | ||
| ) |
Returns the distance between 2 points in 2D.
Definition at line 954 of file geometry.h.
Referenced by mrpt::slam::CGridMapAligner::AlignPDF_robustMatch(), and mrpt::tfest::se2_l2_robust().
◆ distanceBetweenPoints() [2/2]
| T mrpt::math::distanceBetweenPoints | ( | const T | x1, |
| const T | y1, | ||
| const T | z1, | ||
| const T | x2, | ||
| const T | y2, | ||
| const T | z2 | ||
| ) |
Returns the distance between 2 points in 3D.
Definition at line 961 of file geometry.h.
◆ distancePointToPolygon2D()
| double mrpt::math::distancePointToPolygon2D | ( | const double & | px, |
| const double & | py, | ||
| unsigned int | polyEdges, | ||
| const double * | poly_xs, | ||
| const double * | poly_ys | ||
| ) |
Returns the closest distance of a given 2D point to a polygon, or "0" if the point is INTO the polygon or its perimeter.
Definition at line 268 of file geometry.cpp.
References min, mrpt::math::minimumDistanceFromPointToSegment(), and mrpt::math::pointIntoPolygon2D().

◆ distanceSqrBetweenPoints() [1/2]
| T mrpt::math::distanceSqrBetweenPoints | ( | const T | x1, |
| const T | y1, | ||
| const T | x2, | ||
| const T | y2 | ||
| ) |
Returns the square distance between 2 points in 2D.
Definition at line 969 of file geometry.h.
References mrpt::math::square(), z1, and z2.

◆ distanceSqrBetweenPoints() [2/2]
| T mrpt::math::distanceSqrBetweenPoints | ( | const T | x1, |
| const T | y1, | ||
| const T | z1, | ||
| const T | x2, | ||
| const T | y2, | ||
| const T | z2 | ||
| ) |
Returns the square distance between 2 points in 3D.
Definition at line 976 of file geometry.h.
◆ generateAxisBaseFromDirection()
| CMatrixTemplateNumeric<T> mrpt::math::generateAxisBaseFromDirection | ( | T | dx, |
| T | dy, | ||
| T | dz | ||
| ) |
Computes an axis base (a set of three 3D normal vectors) with the given vector being the first of them ("X") NOTE: Make sure of passing all floats or doubles and that the template of the receiving matrix is of the same type!
If ![$ d = [ dx ~ dy ~ dz ] $](form_31.png) is the input vector, then this function returns a matrix
is the input vector, then this function returns a matrix  such as:
such as:
![\[ M = \left( \begin{array}{c c c} v^1_x ~ v^2_x ~ v^3_x \\ v^1_y ~ v^2_y ~ v^3_y \\ v^1_z ~ v^2_z ~ v^3_z \end{array} \right) \]](form_33.png)
And the three normal vectors are computed as:
![\[ v^1 = \frac{d}{|d|} \]](form_34.png)
If (dx!=0 or dy!=0):
![\[ v^2 = \frac{[-dy ~ dx ~ 0 ]}{\sqrt{dx^2+dy^2}} \]](form_35.png)
otherwise (the direction vector is vertical):
![\[ v^2 = [1 ~ 0 ~ 0] \]](form_36.png)
And finally, the third vector is the cross product of the others:
![\[ v^3 = v^1 \times v^2 \]](form_37.png)
- Returns
- The 3x3 matrix (CMatrixTemplateNumeric<T>), containing one vector per column. Throws an std::exception on invalid input (i.e. null direction vector)
(JLB @ 18-SEP-2007)
Definition at line 1121 of file geometry.h.
References mrpt::math::crossProduct3D(), MRPT_END, MRPT_START, mrpt::math::square(), and THROW_EXCEPTION.
Referenced by mrpt::maps::CBeacon::generateRingSOG(), and mrpt::maps::CLandmarksMap::loadSiftFeaturesFromImageObservation().

◆ generateAxisBaseFromDirectionAndAxis()
| void mrpt::math::generateAxisBaseFromDirectionAndAxis | ( | const double(&) | vec[3], |
| char | coord, | ||
| CMatrixDouble & | matrix | ||
| ) |
Creates a homogeneus matrix (4x4) such that the coordinate given (0 for x, 1 for y, 2 for z) corresponds to the provided vector.
- Parameters
-
[in] vec must be a unitary vector
Definition at line 2073 of file geometry.cpp.
References geometryEpsilon.
Referenced by mrpt::math::TPlane::getAsPose3D(), and mrpt::math::TPlane::getAsPose3DForcingOrigin().
◆ getAngle() [1/5]
Computes the angle between two planes.
Definition at line 863 of file geometry.cpp.
References mrpt::math::TPlane::coefs, geometryEpsilon, and M_PI.
Referenced by mrpt::math::TPlane::contains(), mrpt::math::distance(), mrpt::math::TPlane::distance(), and mrpt::math::getAngle().
◆ getAngle() [2/5]
Computes the angle between a plane and a 3D line or segment (implicit constructor will be used if passing a segment instead of a line).
Definition at line 880 of file geometry.cpp.
References mrpt::math::TPlane::coefs, mrpt::math::TLine3D::director, geometryEpsilon, M_PI, and mrpt::utils::sign().

◆ getAngle() [3/5]
Computes the angle between a 3D line or segment and a plane (implicit constructor will be used if passing a segment instead of a line).
Definition at line 223 of file geometry.h.
References mrpt::math::getAngle().

◆ getAngle() [4/5]
Computes the angle between two 3D lines or segments (implicit constructor will be used if passing a segment instead of a line).
Definition at line 897 of file geometry.cpp.
References mrpt::math::TLine3D::director, geometryEpsilon, and M_PI.
◆ getAngle() [5/5]
Computes the angle between two 2D lines or segments (implicit constructor will be used if passing a segment instead of a line).
Definition at line 914 of file geometry.cpp.
References mrpt::math::TLine2D::coefs, geometryEpsilon, and M_PI.
◆ getAngleBisector() [1/2]
Gets the bisector of two lines or segments (implicit constructor will be used if necessary)
Definition at line 2530 of file geometry.cpp.
References mrpt::math::TLine2D::coefs, geometryEpsilon, mrpt::math::intersect(), mrpt::math::square(), and mrpt::math::TLine2D::unitarize().
Referenced by mrpt::math::getAngleBisector().


◆ getAngleBisector() [2/2]
Gets the bisector of two lines or segments (implicit constructor will be used if necessary)
- Exceptions
-
std::logic_error if the lines do not fit in a single plane.
Definition at line 2568 of file geometry.cpp.
References mrpt::math::getAngleBisector(), and mrpt::math::project3D().
◆ getEpsilon()
| double mrpt::mrpt::math::getEpsilon | ( | ) |
Gets the value of the geometric epsilon (default = 1e-5)
- See also
- setEpsilon
Definition at line 30 of file geometry.cpp.
References geometryEpsilon.
Referenced by mrpt::math::TSegment2D::contains(), mrpt::math::TSegment3D::contains(), mrpt::math::TLine2D::contains(), mrpt::math::TLine3D::contains(), mrpt::math::TPlane::contains(), mrpt::math::TPolygon3D::contains(), mrpt::math::TPolygon2D::createRegularPolygon(), mrpt::math::TPolygon3D::createRegularPolygon(), mrpt::math::TPlane::distance(), mrpt::math::TLine2D::getAsPose2D(), mrpt::math::TPlane::getAsPose3D(), getHeight(), mrpt::math::TPolygon2D::isConvex(), mrpt::math::removeRepVertices(), mrpt::math::removeUnusedVertices(), solveEqn(), mrpt::math::TLine2D::TLine2D(), mrpt::math::TLine3D::TLine3D(), mrpt::math::TPlane::TPlane(), mrpt::opengl::CCylinder::traceRay(), and mrpt::math::vectorsAreParallel3D().
◆ getPrismBounds()
| void mrpt::math::getPrismBounds | ( | const std::vector< TPoint3D > & | poly, |
| TPoint3D & | pMin, | ||
| TPoint3D & | pMax | ||
| ) |
Gets the prism bounds of a 3D polygon or set of 3D points.
Definition at line 2015 of file geometry.cpp.
References min, mrpt::math::TPoint3D::x, mrpt::math::TPoint3D::y, and mrpt::math::TPoint3D::z.
Referenced by mrpt::math::TPolygon3D::contains(), getMinAndMaxBounds(), and mrpt::math::intersect().

◆ getRectangleBounds()
| void mrpt::math::getRectangleBounds | ( | const std::vector< TPoint2D > & | poly, |
| TPoint2D & | pMin, | ||
| TPoint2D & | pMax | ||
| ) |
Gets the rectangular bounds of a 2D polygon or set of 2D points.
Definition at line 1900 of file geometry.cpp.
References min, mrpt::math::TPoint2D::x, and mrpt::math::TPoint2D::y.
◆ getRegressionLine() [1/2]
Using eigenvalues, gets the best fitting line for a set of 2D points.
Returns an estimation of the error.
- See also
- spline, leastSquareLinearFit
Definition at line 2109 of file geometry.cpp.
References mrpt::math::TLine2D::coefs, and mrpt::math::covariancesAndMean().

◆ getRegressionLine() [2/2]
Using eigenvalues, gets the best fitting line for a set of 3D points.
Returns an estimation of the error.
- See also
- spline, leastSquareLinearFit
Definition at line 2137 of file geometry.cpp.
References mrpt::math::covariancesAndMean(), mrpt::math::TLine3D::director, getIndexOfMax(), and mrpt::math::TLine3D::pBase.

◆ getRegressionPlane()
Using eigenvalues, gets the best fitting plane for a set of 3D points.
Returns an estimation of the error.
- See also
- spline, leastSquareLinearFit
Definition at line 2157 of file geometry.cpp.
References mrpt::math::TPlane::coefs, mrpt::math::covariancesAndMean(), geometryEpsilon, and getIndexOfMin().
Referenced by mrpt::detectors::CFaceDetection::checkIfFacePlane(), mrpt::math::conformAPlane(), mrpt::math::TPolygon3D::getBestFittingPlane(), and getPlanes().


◆ getSegmentBisector() [1/2]
| void mrpt::math::getSegmentBisector | ( | const TSegment2D & | sgm, |
| TLine2D & | bis | ||
| ) |
Gets the bisector of a 2D segment.
Definition at line 2508 of file geometry.cpp.
References mrpt::math::TLine2D::coefs, mrpt::math::TSegment2D::getCenter(), mrpt::math::TSegment2D::point1, mrpt::math::TSegment2D::point2, mrpt::math::TLine2D::unitarize(), mrpt::math::TPoint2D::x, and mrpt::math::TPoint2D::y.
◆ getSegmentBisector() [2/2]
| void mrpt::math::getSegmentBisector | ( | const TSegment3D & | sgm, |
| TPlane & | bis | ||
| ) |
Gets the bisector of a 3D segment.
Definition at line 2518 of file geometry.cpp.
References mrpt::math::TPlane::coefs, mrpt::math::TSegment3D::getCenter(), mrpt::math::TSegment3D::point1, mrpt::math::TSegment3D::point2, mrpt::math::TPlane::unitarize(), mrpt::math::TPoint3D::x, mrpt::math::TPoint3D::y, and mrpt::math::TPoint3D::z.
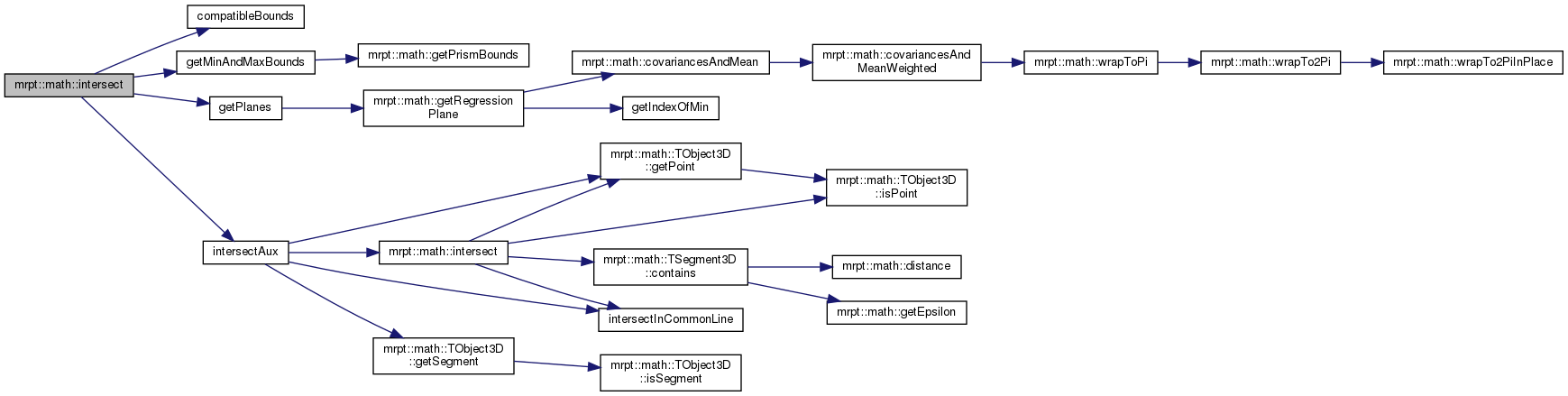
◆ intersect() [1/31]
| bool mrpt::math::intersect | ( | const TSegment3D & | s1, |
| const TSegment3D & | s2, | ||
| TObject3D & | obj | ||
| ) |
Gets the intersection between two 3D segments.
Possible outcomes:
- Segments intersect: Return=true, obj.getType()=GEOMETRIC_TYPE_POINT
- Segments don't intersect & are parallel: Return=true, obj.getType()=GEOMETRIC_TYPE_SEGMENT, obj is the segment "in between" both segments.
- Segments don't intersect & aren't parallel: Return=false.
- See also
- TObject3D
Definition at line 635 of file geometry.cpp.
References mrpt::math::TSegment3D::contains(), mrpt::math::TObject3D::getPoint(), intersectInCommonLine(), and mrpt::math::TObject3D::isPoint().
Referenced by mrpt::math::getAngleBisector(), mrpt::opengl::CPolyhedron::getIntersection(), getPlanesIntersection(), mrpt::math::intersect(), intersect(), intersectAux(), mrpt::maps::CHeightGridMap2D_Base::intersectLine3D(), mrpt::math::splitInConvexComponents(), TEST(), and mrpt::math::traceRay().

◆ intersect() [2/31]
| bool mrpt::math::intersect | ( | const TSegment3D & | s1, |
| const TPlane & | p2, | ||
| TObject3D & | obj | ||
| ) |
Gets the intersection between a 3D segment and a plane.
Possible outcomes:
- Don't intersect: Return=false
- s1 is within the plane: Return=true, obj.getType()=GEOMETRIC_TYPE_SEGMENT
- s1 intersects the plane at one point: Return=true, obj.getType()=GEOMETRIC_TYPE_POINT
- See also
- TObject3D
Definition at line 657 of file geometry.cpp.
References mrpt::math::TSegment3D::contains(), and mrpt::math::intersect().
◆ intersect() [3/31]
| bool mrpt::math::intersect | ( | const TSegment3D & | s1, |
| const TLine3D & | r2, | ||
| TObject3D & | obj | ||
| ) |
Gets the intersection between a 3D segment and a 3D line.
Possible outcomes:
- They don't intersect : Return=false
- s1 lies within the line: Return=true, obj.getType()=GEOMETRIC_TYPE_SEGMENT
- s1 intersects the line at a point: Return=true, obj.getType()=GEOMETRIC_TYPE_POINT
- See also
- TObject3D
Definition at line 676 of file geometry.cpp.
References mrpt::math::TSegment3D::contains(), and mrpt::math::intersect().
◆ intersect() [4/31]
|
inline |
Gets the intersection between a plane and a 3D segment.
Possible outcomes:
- Don't intersect: Return=false
- s2 is within the plane: Return=true, obj.getType()=GEOMETRIC_TYPE_SEGMENT
- s2 intersects the plane at one point: Return=true, obj.getType()=GEOMETRIC_TYPE_POINT
- See also
- TObject3D
Definition at line 100 of file geometry.h.
References mrpt::math::intersect().
◆ intersect() [5/31]
Gets the intersection between two planes.
Possible outcomes:
- Planes are parallel: Return=false
- Planes intersect into a line: Return=true, obj.getType()=GEOMETRIC_TYPE_LINE
- See also
- TObject3D
Definition at line 695 of file geometry.cpp.
References mrpt::math::TPlane::coefs, mrpt::math::crossProduct3D(), mrpt::math::TLine3D::director, geometryEpsilon, mrpt::math::TLine3D::pBase, and mrpt::math::TLine3D::unitarize().

◆ intersect() [6/31]
Gets the intersection between a plane and a 3D line.
Possible outcomes:
- Line is parallel to plane but not within it: Return=false
- Line is contained in the plane: Return=true, obj.getType()=GEOMETRIC_TYPE_LINE
- Line intersects the plane at one point: Return=true, obj.getType()=GEOMETRIC_TYPE_POINT
- See also
- TObject3D
Definition at line 738 of file geometry.cpp.
References mrpt::math::TPlane::coefs, mrpt::math::TLine3D::director, mrpt::math::TPlane::evaluatePoint(), geometryEpsilon, mrpt::math::TLine3D::pBase, mrpt::math::TPoint3D::x, mrpt::math::TPoint3D::y, and mrpt::math::TPoint3D::z.

◆ intersect() [7/31]
|
inline |
Gets the intersection between a 3D line and a 3D segment.
Possible outcomes:
- They don't intersect : Return=false
- s2 lies within the line: Return=true, obj.getType()=GEOMETRIC_TYPE_SEGMENT
- s2 intersects the line at a point: Return=true, obj.getType()=GEOMETRIC_TYPE_POINT
- See also
- TObject3D
Definition at line 131 of file geometry.h.
References mrpt::math::intersect().
◆ intersect() [8/31]
Gets the intersection between a 3D line and a plane.
Possible outcomes:
- Line is parallel to plane but not within it: Return=false
- Line is contained in the plane: Return=true, obj.getType()=GEOMETRIC_TYPE_LINE
- Line intersects the plane at one point: Return=true, obj.getType()=GEOMETRIC_TYPE_POINT
- See also
- TObject3D
Definition at line 144 of file geometry.h.
References mrpt::math::intersect().
◆ intersect() [9/31]
Gets the intersection between two 3D lines.
Possible outcomes:
- Lines do not intersect: Return=false
- Lines are parallel and do not coincide: Return=false
- Lines coincide (are the same): Return=true, obj.getType()=GEOMETRIC_TYPE_LINE
- Lines intesect in a point: Return=true, obj.getType()=GEOMETRIC_TYPE_POINT
- See also
- TObject3D
Definition at line 770 of file geometry.cpp.
References mrpt::math::TLine3D::contains(), mrpt::math::TLine3D::director, geometryEpsilon, and mrpt::math::TLine3D::pBase.

◆ intersect() [10/31]
Gets the intersection between two 2D lines.
Possible outcomes:
- Lines do not intersect: Return=false
- Lines are parallel and do not coincide: Return=false
- Lines coincide (are the same): Return=true, obj.getType()=GEOMETRIC_TYPE_LINE
- Lines intesect in a point: Return=true, obj.getType()=GEOMETRIC_TYPE_POINT
- See also
- TObject2D
Definition at line 807 of file geometry.cpp.
References mrpt::math::TLine2D::coefs, and geometryEpsilon.
◆ intersect() [11/31]
| bool mrpt::math::intersect | ( | const TLine2D & | r1, |
| const TSegment2D & | s2, | ||
| TObject2D & | obj | ||
| ) |
Gets the intersection between a 2D line and a 2D segment.
Possible outcomes:
- They don't intersect: Return=false
- s2 lies within the line: Return=true, obj.getType()=GEOMETRIC_TYPE_SEGMENT
- Both intersects in one point: Return=true, obj.getType()=GEOMETRIC_TYPE_POINT
- See also
- TObject2D
Definition at line 834 of file geometry.cpp.
References mrpt::math::TSegment2D::contains(), and mrpt::math::intersect().
◆ intersect() [12/31]
|
inline |
Gets the intersection between a 2D line and a 2D segment.
Possible outcomes:
- They don't intersect: Return=false
- s1 lies within the line: Return=true, obj.getType()=GEOMETRIC_TYPE_SEGMENT
- Both intersects in one point: Return=true, obj.getType()=GEOMETRIC_TYPE_POINT
- See also
- TObject2D
Definition at line 189 of file geometry.h.
References mrpt::math::intersect().
◆ intersect() [13/31]
| bool mrpt::math::intersect | ( | const TSegment2D & | s1, |
| const TSegment2D & | s2, | ||
| TObject2D & | obj | ||
| ) |
Gets the intersection between two 2D segments.
Possible outcomes:
- Segments intersect: Return=true, obj.getType()=GEOMETRIC_TYPE_POINT
- Segments don't intersect & are parallel: Return=true, obj.getType()=GEOMETRIC_TYPE_SEGMENT, obj is the segment "in between" both segments.
- Segments don't intersect & aren't parallel: Return=false.
- See also
- TObject2D
Definition at line 849 of file geometry.cpp.
References mrpt::math::TSegment2D::contains(), mrpt::math::intersect(), and intersectInCommonLine().
◆ intersect() [14/31]
| bool mrpt::math::intersect | ( | const TPolygon2D & | p1, |
| const TSegment2D & | s2, | ||
| TObject2D & | obj | ||
| ) |
Gets the intersection between a 2D polygon and a 2D segment.
- See also
- TObject2D
Definition at line 1242 of file geometry.cpp.
References mrpt::math::TSegment2D::contains(), mrpt::math::intersect(), and intersectInCommonLine().
◆ intersect() [15/31]
| bool mrpt::math::intersect | ( | const TPolygon2D & | p1, |
| const TLine2D & | r2, | ||
| TObject2D & | obj | ||
| ) |
Gets the intersection between a 2D polygon and a 2D line.
- See also
- TObject2D
Definition at line 1255 of file geometry.cpp.
References geometryEpsilon, mrpt::math::TLine2D::getAsPose2D(), mrpt::math::project2D(), and mrpt::utils::sign().
◆ intersect() [16/31]
| bool mrpt::math::intersect | ( | const TPolygon2D & | p1, |
| const TPolygon2D & | p2, | ||
| TObject2D & | obj | ||
| ) |
Gets the intersection between two 2D polygons.
- See also
- TObject2D
Definition at line 1464 of file geometry.cpp.
References fromObject(), mrpt::math::CSparseMatrixTemplate< T >::getColCount(), mrpt::math::CSparseMatrixTemplate< T >::getRowCount(), getSegmentsWithLine(), mrpt::math::intersect(), and THROW_EXCEPTION.
◆ intersect() [17/31]
|
inline |
Gets the intersection between a 2D segment and a 2D polygon.
- See also
- TObject2D
Definition at line 477 of file geometry.h.
◆ intersect() [18/31]
|
inline |
Gets the intersection between a 2D line and a 2D polygon.
- See also
- TObject2D
Definition at line 483 of file geometry.h.
References mrpt::math::intersect().
◆ intersect() [19/31]
| bool mrpt::math::intersect | ( | const TPolygon3D & | p1, |
| const TSegment3D & | s2, | ||
| TObject3D & | obj | ||
| ) |
Gets the intersection between a 3D polygon and a 3D segment.
- See also
- TObject3D
Definition at line 1512 of file geometry.cpp.
References mrpt::math::TPolygon2D::contains(), mrpt::math::TPolygon3D::getPlane(), mrpt::math::intersect(), and mrpt::math::project3D().
◆ intersect() [20/31]
| bool mrpt::math::intersect | ( | const TPolygon3D & | p1, |
| const TLine3D & | r2, | ||
| TObject3D & | obj | ||
| ) |
Gets the intersection between a 3D polygon and a 3D line.
- See also
- TObject3D
Definition at line 1535 of file geometry.cpp.
References mrpt::math::TPolygon2D::contains(), mrpt::math::TPolygon3D::getPlane(), mrpt::math::intersect(), and mrpt::math::project3D().
◆ intersect() [21/31]
| bool mrpt::math::intersect | ( | const TPolygon3D & | p1, |
| const TPlane & | p2, | ||
| TObject3D & | obj | ||
| ) |
Gets the intersection between a 3D polygon and a plane.
- See also
- TObject3D
Definition at line 1557 of file geometry.cpp.
References mrpt::math::TPolygon3D::getPlane(), and mrpt::math::intersect().
◆ intersect() [22/31]
| bool mrpt::math::intersect | ( | const TPolygon3D & | p1, |
| const TPolygon3D & | p2, | ||
| TObject3D & | obj | ||
| ) |
Gets the intersection between two 3D polygons.
- See also
- TObject3D
Definition at line 1616 of file geometry.cpp.
References compatibleBounds(), mrpt::math::TPolygon3D::getPlane(), mrpt::math::getPrismBounds(), and intersectAux().
◆ intersect() [23/31]
|
inline |
Gets the intersection between a 3D segment and a 3D polygon.
- See also
- TObject3D
Definition at line 498 of file geometry.h.
◆ intersect() [24/31]
|
inline |
Gets the intersection between a 3D line and a 3D polygon.
- See also
- TObject3D
Definition at line 504 of file geometry.h.
References mrpt::math::intersect().
◆ intersect() [25/31]
|
inline |
Gets the intersection between a plane and a 3D polygon.
- See also
- TObject3D
Definition at line 509 of file geometry.h.
References mrpt::math::intersect().
◆ intersect() [26/31]
| size_t mrpt::math::intersect | ( | const std::vector< TPolygon3D > & | v1, |
| const std::vector< TPolygon3D > & | v2, | ||
| CSparseMatrixTemplate< TObject3D > & | objs | ||
| ) |
Gets the intersection between two sets of 3D polygons.
The intersection is returned as an sparse matrix with each pair of polygons' intersections, and the return value is the amount of intersections found.
- See also
- TObject3D,CSparseMatrixTemplate
Definition at line 1657 of file geometry.cpp.
References mrpt::math::CSparseMatrixTemplate< T >::clear(), compatibleBounds(), getMinAndMaxBounds(), mrpt::math::CSparseMatrixTemplate< T >::getNonNullElements(), getPlanes(), intersectAux(), and mrpt::math::CSparseMatrixTemplate< T >::resize().
◆ intersect() [27/31]
| size_t mrpt::math::intersect | ( | const std::vector< TPolygon3D > & | v1, |
| const std::vector< TPolygon3D > & | v2, | ||
| std::vector< TObject3D > & | objs | ||
| ) |
Gets the intersection between two sets of 3D polygons.
The intersection is returned as a vector with every intersection found, and the return value is the amount of intersections found.
- See also
- TObject3D
Definition at line 1681 of file geometry.cpp.
References compatibleBounds(), getMinAndMaxBounds(), getPlanes(), and intersectAux().
◆ intersect() [28/31]
| size_t mrpt::math::intersect | ( | const std::vector< T > & | v1, |
| const std::vector< U > & | v2, | ||
| CSparseMatrixTemplate< O > & | objs | ||
| ) |
Gets the intersection between vectors of geometric objects and returns it in a sparse matrix of either TObject2D or TObject3D.
- See also
- TObject2D,TObject3D,CSparseMatrix
Definition at line 537 of file geometry.h.
References mrpt::math::CSparseMatrixTemplate< T >::clear(), mrpt::math::CSparseMatrixTemplate< T >::getNonNullElements(), mrpt::math::intersect(), and mrpt::math::CSparseMatrixTemplate< T >::resize().

◆ intersect() [29/31]
| size_t mrpt::math::intersect | ( | const std::vector< T > & | v1, |
| const std::vector< U > & | v2, | ||
| std::vector< O > | objs | ||
| ) |
◆ intersect() [30/31]
Gets the intersection between any pair of 2D objects.
Definition at line 1715 of file geometry.cpp.
References mrpt::math::TSegment2D::contains(), mrpt::math::TLine2D::contains(), mrpt::math::TPolygon2D::contains(), mrpt::math::distance(), geometryEpsilon, mrpt::math::TObject2D::getLine(), mrpt::math::TObject2D::getPoint(), mrpt::math::TObject2D::getPolygon(), mrpt::math::TObject2D::getSegment(), and mrpt::math::intersect().

◆ intersect() [31/31]
Gets the intersection between any pair of 3D objects.
Definition at line 1787 of file geometry.cpp.
References mrpt::math::TSegment3D::contains(), mrpt::math::TLine3D::contains(), mrpt::math::TPlane::contains(), mrpt::math::TPolygon3D::contains(), mrpt::math::distance(), geometryEpsilon, mrpt::math::TObject3D::getLine(), mrpt::math::TObject3D::getPlane(), mrpt::math::TObject3D::getPoint(), mrpt::math::TObject3D::getPolygon(), mrpt::math::TObject3D::getSegment(), and mrpt::math::intersect().

◆ minDistBetweenLines()
| bool mrpt::math::minDistBetweenLines | ( | const double & | p1_x, |
| const double & | p1_y, | ||
| const double & | p1_z, | ||
| const double & | p2_x, | ||
| const double & | p2_y, | ||
| const double & | p2_z, | ||
| const double & | p3_x, | ||
| const double & | p3_y, | ||
| const double & | p3_z, | ||
| const double & | p4_x, | ||
| const double & | p4_y, | ||
| const double & | p4_z, | ||
| double & | x, | ||
| double & | y, | ||
| double & | z, | ||
| double & | dist | ||
| ) |
Calculates the minimum distance between a pair of lines.
The lines are given by:
- Line 1 = P1 + f (P2-P1)
- Line 2 = P3 + f (P4-P3) The Euclidean distance is returned in "dist", and the mid point between the lines in (x,y,z)
- Returns
- It returns false if there is no solution, i.e. lines are (almost, up to EPS) parallel.
Definition at line 302 of file geometry.cpp.
References mrpt::math::square().

◆ minimumDistanceFromPointToSegment()
| double mrpt::math::minimumDistanceFromPointToSegment | ( | const double | Px, |
| const double | Py, | ||
| const double | x1, | ||
| const double | y1, | ||
| const double | x2, | ||
| const double | y2, | ||
| T & | out_x, | ||
| T & | out_y | ||
| ) |
Computes the closest point from a given point to a segment, and returns that minimum distance.
Definition at line 986 of file geometry.h.
References mrpt::math::square(), z1, and z2.
Referenced by mrpt::math::distancePointToPolygon2D(), and mrpt::nav::CHolonomicND::evaluateGaps().


◆ operator!=() [1/6]
|
inline |
Exact comparison between 2D points.
Definition at line 892 of file lightweight_geom_data.h.
References mrpt::math::TPoint2D::x, and mrpt::math::TPoint2D::y.
◆ operator!=() [2/6]
|
inline |
Exact comparison between 3D points.
Definition at line 906 of file lightweight_geom_data.h.
References mrpt::math::TPoint3D::x, mrpt::math::TPoint3D::y, and mrpt::math::TPoint3D::z.
◆ operator!=() [3/6]
|
inline |
Exact comparison between 2D poses, taking possible cycles into account.
Definition at line 922 of file lightweight_geom_data.h.
References mrpt::math::TPose2D::phi, mrpt::math::wrapTo2Pi(), mrpt::math::TPose2D::x, and mrpt::math::TPose2D::y.

◆ operator!=() [4/6]
|
inline |
Exact comparison between 3D poses, taking possible cycles into account.
Definition at line 943 of file lightweight_geom_data.h.
References mrpt::math::TPose3D::pitch, mrpt::math::TPose3D::roll, mrpt::math::wrapTo2Pi(), mrpt::math::TPose3D::x, mrpt::math::TPose3D::y, mrpt::math::TPose3D::yaw, and mrpt::math::TPose3D::z.

◆ operator!=() [5/6]
|
inline |
Definition at line 1141 of file lightweight_geom_data.h.
References mrpt::math::TSegment2D::point1, and mrpt::math::TSegment2D::point2.
◆ operator!=() [6/6]
|
inline |
Definition at line 1151 of file lightweight_geom_data.h.
References mrpt::math::TSegment3D::point1, and mrpt::math::TSegment3D::point2.
◆ operator-()
Unary minus operator for 3D points.
Definition at line 878 of file lightweight_geom_data.h.
References mrpt::math::TPoint3D::x, mrpt::math::TPoint3D::y, and mrpt::math::TPoint3D::z.
◆ operator<<() [1/18]
| std::ostream & mrpt::math::operator<< | ( | std::ostream & | o, |
| const TPoint2D & | p | ||
| ) |
Definition at line 337 of file lightweight_geom_data.cpp.
◆ operator<<() [2/18]
| std::ostream & mrpt::math::operator<< | ( | std::ostream & | o, |
| const TPoint3D & | p | ||
| ) |
Definition at line 341 of file lightweight_geom_data.cpp.
◆ operator<<() [3/18]
| std::ostream & mrpt::math::operator<< | ( | std::ostream & | o, |
| const TPose2D & | p | ||
| ) |
Definition at line 345 of file lightweight_geom_data.cpp.
◆ operator<<() [4/18]
| std::ostream & mrpt::math::operator<< | ( | std::ostream & | o, |
| const TPose3D & | p | ||
| ) |
Definition at line 349 of file lightweight_geom_data.cpp.
◆ operator<<() [5/18]
| std::ostream & mrpt::math::operator<< | ( | std::ostream & | o, |
| const TPose3DQuat & | p | ||
| ) |
Definition at line 353 of file lightweight_geom_data.cpp.
◆ operator<<() [6/18]
| mrpt::utils::CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TPoint2D & | o | ||
| ) |
Definition at line 1359 of file lightweight_geom_data.cpp.
References mrpt::math::TPoint2D::x, and mrpt::math::TPoint2D::y.
◆ operator<<() [7/18]
| mrpt::utils::CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TPoint3D & | o | ||
| ) |
Definition at line 1372 of file lightweight_geom_data.cpp.
References mrpt::math::TPoint3D::x, mrpt::math::TPoint3D::y, and mrpt::math::TPoint3D::z.
◆ operator<<() [8/18]
| mrpt::utils::CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TPose2D & | o | ||
| ) |
Definition at line 1385 of file lightweight_geom_data.cpp.
References mrpt::math::TPose2D::phi, mrpt::math::TPose2D::x, and mrpt::math::TPose2D::y.
◆ operator<<() [9/18]
| mrpt::utils::CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TPose3D & | o | ||
| ) |
Definition at line 1434 of file lightweight_geom_data.cpp.
References mrpt::math::TPose3D::pitch, mrpt::math::TPose3D::roll, mrpt::math::TPose3D::x, mrpt::math::TPose3D::y, mrpt::math::TPose3D::yaw, and mrpt::math::TPose3D::z.
◆ operator<<() [10/18]
| CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TSegment2D & | s | ||
| ) |
Definition at line 362 of file lightweight_geom_data.cpp.
◆ operator<<() [11/18]
| CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TLine2D & | l | ||
| ) |
Definition at line 370 of file lightweight_geom_data.cpp.
References mrpt::math::TLine2D::coefs.
◆ operator<<() [12/18]
| mrpt::utils::CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TObject2D & | o | ||
| ) |
Definition at line 1487 of file lightweight_geom_data.cpp.
References mrpt::math::GEOMETRIC_TYPE_LINE, mrpt::math::GEOMETRIC_TYPE_POINT, mrpt::math::GEOMETRIC_TYPE_POLYGON, mrpt::math::GEOMETRIC_TYPE_SEGMENT, mrpt::math::TObject2D::getLine(), mrpt::math::TObject2D::getPoint(), mrpt::math::TObject2D::getPolygon(), mrpt::math::TObject2D::getSegment(), and mrpt::math::TObject2D::getType().
◆ operator<<() [13/18]
| mrpt::utils::CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TSegment3D & | s | ||
| ) |
Definition at line 380 of file lightweight_geom_data.cpp.
◆ operator<<() [14/18]
| mrpt::utils::CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TLine3D & | l | ||
| ) |
Definition at line 390 of file lightweight_geom_data.cpp.
References mrpt::math::TLine3D::director, and mrpt::math::TLine3D::pBase.
◆ operator<<() [15/18]
| mrpt::utils::CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TPlane & | p | ||
| ) |
Definition at line 400 of file lightweight_geom_data.cpp.
◆ operator<<() [16/18]
| mrpt::utils::CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TObject3D & | o | ||
| ) |
Definition at line 1574 of file lightweight_geom_data.cpp.
References mrpt::math::GEOMETRIC_TYPE_LINE, mrpt::math::GEOMETRIC_TYPE_PLANE, mrpt::math::GEOMETRIC_TYPE_POINT, mrpt::math::GEOMETRIC_TYPE_POLYGON, mrpt::math::GEOMETRIC_TYPE_SEGMENT, mrpt::math::TObject3D::getLine(), mrpt::math::TObject3D::getPlane(), mrpt::math::TObject3D::getPoint(), mrpt::math::TObject3D::getPolygon(), mrpt::math::TObject3D::getSegment(), and mrpt::math::TObject3D::getType().

◆ operator<<() [17/18]
| mrpt::utils::CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TTwist2D & | o | ||
| ) |
Definition at line 1398 of file lightweight_geom_data.cpp.
References mrpt::math::TTwist2D::size().

◆ operator<<() [18/18]
| mrpt::utils::CStream & mrpt::math::operator<< | ( | mrpt::utils::CStream & | out, |
| const mrpt::math::TTwist3D & | o | ||
| ) |
Definition at line 1411 of file lightweight_geom_data.cpp.
References mrpt::math::TTwist3D::size().

◆ operator==() [1/6]
Exact comparison between 2D points.
Definition at line 885 of file lightweight_geom_data.h.
References mrpt::math::TPoint2D::x, and mrpt::math::TPoint2D::y.
◆ operator==() [2/6]
Exact comparison between 3D points.
Definition at line 899 of file lightweight_geom_data.h.
References mrpt::math::TPoint3D::x, mrpt::math::TPoint3D::y, and mrpt::math::TPoint3D::z.
◆ operator==() [3/6]
Exact comparison between 2D poses, taking possible cycles into account.
Definition at line 913 of file lightweight_geom_data.h.
References mrpt::math::TPose2D::phi, mrpt::math::wrapTo2Pi(), mrpt::math::TPose2D::x, and mrpt::math::TPose2D::y.

◆ operator==() [4/6]
Exact comparison between 3D poses, taking possible cycles into account.
Definition at line 931 of file lightweight_geom_data.h.
References mrpt::math::TPose3D::pitch, mrpt::math::TPose3D::roll, mrpt::math::wrapTo2Pi(), mrpt::math::TPose3D::x, mrpt::math::TPose3D::y, mrpt::math::TPose3D::yaw, and mrpt::math::TPose3D::z.

◆ operator==() [5/6]
|
inline |
Definition at line 1136 of file lightweight_geom_data.h.
References mrpt::math::TSegment2D::point1, and mrpt::math::TSegment2D::point2.
◆ operator==() [6/6]
|
inline |
Definition at line 1146 of file lightweight_geom_data.h.
References mrpt::math::TSegment3D::point1, and mrpt::math::TSegment3D::point2.
◆ operator>>() [1/13]
| mrpt::utils::CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TPoint2D & | o | ||
| ) |
Definition at line 1353 of file lightweight_geom_data.cpp.
References mrpt::math::TPoint2D::x, and mrpt::math::TPoint2D::y.
◆ operator>>() [2/13]
| mrpt::utils::CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TPoint3D & | o | ||
| ) |
Definition at line 1366 of file lightweight_geom_data.cpp.
References mrpt::math::TPoint3D::x, mrpt::math::TPoint3D::y, and mrpt::math::TPoint3D::z.
◆ operator>>() [3/13]
| mrpt::utils::CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TPose2D & | o | ||
| ) |
Definition at line 1379 of file lightweight_geom_data.cpp.
References mrpt::math::TPose2D::phi, mrpt::math::TPose2D::x, and mrpt::math::TPose2D::y.
◆ operator>>() [4/13]
| mrpt::utils::CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TPose3D & | o | ||
| ) |
Definition at line 1428 of file lightweight_geom_data.cpp.
References mrpt::math::TPose3D::pitch, mrpt::math::TPose3D::roll, mrpt::math::TPose3D::x, mrpt::math::TPose3D::y, mrpt::math::TPose3D::yaw, and mrpt::math::TPose3D::z.
◆ operator>>() [5/13]
| CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TSegment2D & | s | ||
| ) |
Definition at line 358 of file lightweight_geom_data.cpp.
◆ operator>>() [6/13]
| CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TLine2D & | l | ||
| ) |
Definition at line 366 of file lightweight_geom_data.cpp.
References mrpt::math::TLine2D::coefs.
◆ operator>>() [7/13]
| mrpt::utils::CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TObject2D & | o | ||
| ) |
Definition at line 1441 of file lightweight_geom_data.cpp.
References mrpt::math::GEOMETRIC_TYPE_LINE, mrpt::math::GEOMETRIC_TYPE_POINT, mrpt::math::GEOMETRIC_TYPE_POLYGON, mrpt::math::GEOMETRIC_TYPE_SEGMENT, and mrpt::math::GEOMETRIC_TYPE_UNDEFINED.
◆ operator>>() [8/13]
| mrpt::utils::CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TSegment3D & | s | ||
| ) |
Definition at line 375 of file lightweight_geom_data.cpp.
◆ operator>>() [9/13]
| mrpt::utils::CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TLine3D & | l | ||
| ) |
Definition at line 385 of file lightweight_geom_data.cpp.
References mrpt::math::TLine3D::director, and mrpt::math::TLine3D::pBase.
◆ operator>>() [10/13]
| mrpt::utils::CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TPlane & | p | ||
| ) |
Definition at line 395 of file lightweight_geom_data.cpp.
◆ operator>>() [11/13]
| mrpt::utils::CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TObject3D & | o | ||
| ) |
◆ operator>>() [12/13]
| mrpt::utils::CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TTwist2D & | o | ||
| ) |
Definition at line 1392 of file lightweight_geom_data.cpp.
References mrpt::math::TTwist2D::size().

◆ operator>>() [13/13]
| mrpt::utils::CStream & mrpt::math::operator>> | ( | mrpt::utils::CStream & | in, |
| mrpt::math::TTwist3D & | o | ||
| ) |
Definition at line 1405 of file lightweight_geom_data.cpp.
References mrpt::math::TTwist3D::size().

◆ pointIntoPolygon2D()
| bool mrpt::math::pointIntoPolygon2D | ( | const double & | px, |
| const double & | py, | ||
| unsigned int | polyEdges, | ||
| const double * | poly_xs, | ||
| const double * | poly_ys | ||
| ) |
Returns true if the 2D point (px,py) falls INTO the given polygon.
- See also
- pointIntoQuadrangle
Definition at line 237 of file geometry.cpp.
Referenced by mrpt::math::distancePointToPolygon2D().

◆ pointIntoQuadrangle()
| bool mrpt::math::pointIntoQuadrangle | ( | T | x, |
| T | y, | ||
| T | v1x, | ||
| T | v1y, | ||
| T | v2x, | ||
| T | v2y, | ||
| T | v3x, | ||
| T | v3y, | ||
| T | v4x, | ||
| T | v4y | ||
| ) |
Specialized method to check whether a point (x,y) falls into a quadrangle.
- See also
- pointIntoPolygon2D
Definition at line 1022 of file geometry.h.
◆ project2D() [1/8]
| void mrpt::math::project2D | ( | const TPoint2D & | point, |
| const mrpt::poses::CPose2D & | newXpose, | ||
| TPoint2D & | newPoint | ||
| ) |
Uses the given pose 2D to project a point into a new base.
Definition at line 1172 of file geometry.cpp.
Referenced by mrpt::math::intersect(), and mrpt::math::project2D().

◆ project2D() [2/8]
|
inline |
Uses the given pose 2D to project a segment into a new base.
Definition at line 404 of file geometry.h.
◆ project2D() [3/8]
| void mrpt::math::project2D | ( | const TLine2D & | line, |
| const mrpt::poses::CPose2D & | newXpose, | ||
| TLine2D & | newLine | ||
| ) |
Uses the given pose 2D to project a line into a new base.
Definition at line 1179 of file geometry.cpp.
References mrpt::math::TLine2D::coefs, mrpt::poses::CPose2D::phi(), mrpt::poses::CPoseOrPoint< DERIVEDCLASS >::x(), and mrpt::poses::CPoseOrPoint< DERIVEDCLASS >::y().

◆ project2D() [4/8]
| void mrpt::math::project2D | ( | const TPolygon2D & | polygon, |
| const mrpt::poses::CPose2D & | newXpose, | ||
| TPolygon2D & | newPolygon | ||
| ) |
Uses the given pose 2D to project a polygon into a new base.
Definition at line 1191 of file geometry.cpp.
◆ project2D() [5/8]
| void mrpt::math::project2D | ( | const TObject2D & | object, |
| const mrpt::poses::CPose2D & | newXpose, | ||
| TObject2D & | newObject | ||
| ) |
Uses the given pose 2D to project any 2D object into a new base.
Definition at line 1200 of file geometry.cpp.
References mrpt::math::GEOMETRIC_TYPE_LINE, mrpt::math::GEOMETRIC_TYPE_POINT, mrpt::math::GEOMETRIC_TYPE_POLYGON, mrpt::math::GEOMETRIC_TYPE_SEGMENT, and mrpt::math::project2D().

◆ project2D() [6/8]
| void mrpt::math::project2D | ( | const T & | obj, |
| const TLine2D & | newXLine, | ||
| T & | newObj | ||
| ) |
Projects any 2D object into the line's base, using its inverse pose.
If the object is exactly inside the line, this projection will zero its Y coordinate.
- Template Parameters
-
CPOSE2D set to mrpt::poses::CPose2D
Definition at line 431 of file geometry.h.
References mrpt::math::TLine2D::getAsPose2D(), and mrpt::math::project2D().

◆ project2D() [7/8]
| void mrpt::math::project2D | ( | const T & | obj, |
| const TLine2D & | newXLine, | ||
| const TPoint2D & | newOrigin, | ||
| T & | newObj | ||
| ) |
Projects any 2D object into the line's base, using its inverse pose and forcing the position of the new coordinate origin.
If the object is exactly inside the line, this projection will zero its Y coordinate.
- Template Parameters
-
CPOSE2D set to mrpt::poses::CPose2D
Definition at line 444 of file geometry.h.
References mrpt::math::TLine2D::getAsPose2DForcingOrigin(), and mrpt::math::project2D().

◆ project2D() [8/8]
| void mrpt::math::project2D | ( | const std::vector< T > & | objs, |
| const mrpt::poses::CPose2D & | newXpose, | ||
| std::vector< T > & | newObjs | ||
| ) |
Projects a set of 2D objects into the line's base.
Definition at line 454 of file geometry.h.
◆ project3D() [1/9]
|
inline |
Uses the given pose 3D to project a point into a new base.
Definition at line 329 of file geometry.h.
Referenced by mrpt::math::TPolygon3D::contains(), mrpt::math::TPolygon3D::distance(), mrpt::math::getAngleBisector(), mrpt::math::intersect(), intersect(), intersectInCommonPlane(), FUnprojectPolygon2D::operator()(), mrpt::math::project3D(), and mrpt::math::splitInConvexComponents().

◆ project3D() [2/9]
|
inline |
Uses the given pose 3D to project a segment into a new base.
Definition at line 337 of file geometry.h.
◆ project3D() [3/9]
| void mrpt::math::project3D | ( | const TLine3D & | line, |
| const mrpt::poses::CPose3D & | newXYpose, | ||
| TLine3D & | newLine | ||
| ) |
Uses the given pose 3D to project a line into a new base.
Definition at line 1075 of file geometry.cpp.
References mrpt::poses::CPose3D::composePoint(), mrpt::math::TLine3D::director, mrpt::poses::CPose3D::getHomogeneousMatrixVal(), mrpt::math::TLine3D::pBase, mrpt::math::TLine3D::unitarize(), mrpt::math::TPoint3D::x, mrpt::math::TPoint3D::y, and mrpt::math::TPoint3D::z.
◆ project3D() [4/9]
| void mrpt::math::project3D | ( | const TPlane & | plane, |
| const mrpt::poses::CPose3D & | newXYpose, | ||
| TPlane & | newPlane | ||
| ) |
Uses the given pose 3D to project a plane into a new base.
Definition at line 1091 of file geometry.cpp.
References mrpt::math::TPlane::coefs, mrpt::math::TPlane::evaluatePoint(), mrpt::poses::CPose3D::getHomogeneousMatrixVal(), and mrpt::math::TPlane::unitarize().

◆ project3D() [5/9]
| void mrpt::math::project3D | ( | const TPolygon3D & | polygon, |
| const mrpt::poses::CPose3D & | newXYpose, | ||
| TPolygon3D & | newPolygon | ||
| ) |
Uses the given pose 3D to project a polygon into a new base.
Definition at line 1113 of file geometry.cpp.
References mrpt::math::project3D().

◆ project3D() [6/9]
| void mrpt::math::project3D | ( | const TObject3D & | object, |
| const mrpt::poses::CPose3D & | newXYPose, | ||
| TObject3D & | newObject | ||
| ) |
Uses the given pose 3D to project any 3D object into a new base.
Definition at line 1122 of file geometry.cpp.
References mrpt::math::GEOMETRIC_TYPE_LINE, mrpt::math::GEOMETRIC_TYPE_PLANE, mrpt::math::GEOMETRIC_TYPE_POINT, mrpt::math::GEOMETRIC_TYPE_POLYGON, mrpt::math::GEOMETRIC_TYPE_SEGMENT, and mrpt::math::project3D().

◆ project3D() [7/9]
| void mrpt::math::project3D | ( | const T & | obj, |
| const TPlane & | newXYPlane, | ||
| T & | newObj | ||
| ) |
Projects any 3D object into the plane's base, using its inverse pose.
If the object is exactly inside the plane, this projection will zero its Z coordinates
Definition at line 366 of file geometry.h.
References mrpt::math::TPlane::getAsPose3D(), and mrpt::math::project3D().
◆ project3D() [8/9]
| void mrpt::math::project3D | ( | const T & | obj, |
| const TPlane & | newXYPlane, | ||
| const TPoint3D & | newOrigin, | ||
| T & | newObj | ||
| ) |
Projects any 3D object into the plane's base, using its inverse pose and forcing the position of the new coordinates origin.
If the object is exactly inside the plane, this projection will zero its Z coordinates
Definition at line 377 of file geometry.h.
References mrpt::math::TPlane::getAsPose3D(), and mrpt::math::project3D().
◆ project3D() [9/9]
| void mrpt::math::project3D | ( | const std::vector< T > & | objs, |
| const mrpt::poses::CPose3D & | newXYpose, | ||
| std::vector< T > & | newObjs | ||
| ) |
Projects a set of 3D objects into the plane's base.
Definition at line 389 of file geometry.h.
◆ RectanglesIntersection()
| bool mrpt::math::RectanglesIntersection | ( | const double & | R1_x_min, |
| const double & | R1_x_max, | ||
| const double & | R1_y_min, | ||
| const double & | R1_y_max, | ||
| const double & | R2_x_min, | ||
| const double & | R2_x_max, | ||
| const double & | R2_y_min, | ||
| const double & | R2_y_max, | ||
| const double & | R2_pose_x, | ||
| const double & | R2_pose_y, | ||
| const double & | R2_pose_phi | ||
| ) |
Returns whether two rotated rectangles intersect.
The first rectangle is not rotated and given by (R1_x_min,R1_x_max)-(R1_y_min,R1_y_max). The second rectangle is given is a similar way, but it is internally rotated according to the given coordinates translation (R2_pose_x,R2_pose_y,R2_pose_phi(radians)), relative to the coordinates system of rectangle 1.
Definition at line 373 of file geometry.cpp.
References mrpt::math::CPolygon::AddVertex(), mrpt::math::CPolygon::PointIntoPolygon(), and mrpt::math::SegmentsIntersection().
Referenced by mrpt::hmtslam::CHierarchicalMapMHPartition::computeOverlapProbabilityBetweenNodes().


◆ SegmentsIntersection() [1/2]
| bool mrpt::math::SegmentsIntersection | ( | const double | x1, |
| const double | y1, | ||
| const double | x2, | ||
| const double | y2, | ||
| const double | x3, | ||
| const double | y3, | ||
| const double | x4, | ||
| const double | y4, | ||
| double & | ix, | ||
| double & | iy | ||
| ) |
Returns the intersection point, and if it exists, between two segments.
Definition at line 124 of file geometry.cpp.
Referenced by mrpt::math::RectanglesIntersection(), and mrpt::math::SegmentsIntersection().

◆ SegmentsIntersection() [2/2]
| bool mrpt::math::SegmentsIntersection | ( | const double | x1, |
| const double | y1, | ||
| const double | x2, | ||
| const double | y2, | ||
| const double | x3, | ||
| const double | y3, | ||
| const double | x4, | ||
| const double | y4, | ||
| float & | ix, | ||
| float & | iy | ||
| ) |
Returns the intersection point, and if it exists, between two segments.
Definition at line 222 of file geometry.cpp.
References mrpt::math::SegmentsIntersection().

◆ setEpsilon()
| void mrpt::mrpt::math::setEpsilon | ( | double | nE | ) |
Changes the value of the geometric epsilon (default = 1e-5)
- See also
- geometryEpsilon,getEpsilon
Definition at line 34 of file geometry.cpp.
References eps, and geometryEpsilon.
◆ skew_symmetric3() [1/2]
|
inline |
Computes the 3x3 skew symmetric matrix from a 3-vector or 3-array:
![\[ M([x ~ y ~ z]^\top) = \left( \begin{array}{c c c} 0 & -z & y \\ z & 0 & -x \\ -y & x & 0 \end{array} \right) \]](form_29.png)
.
Definition at line 853 of file geometry.h.
References ASSERT_.
Referenced by mrpt::poses::CPose3DRotVec::composeFrom(), mrpt::poses::dVinvt_dR(), mrpt::poses::CPose3D::ln_jacob(), and TEST().
◆ skew_symmetric3() [2/2]
|
inline |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
Definition at line 869 of file geometry.h.
◆ skew_symmetric3_neg() [1/2]
|
inline |
Computes the negative version of a 3x3 skew symmetric matrix from a 3-vector or 3-array:
![\[ -M([x ~ y ~ z]^\top) = \left( \begin{array}{c c c} 0 & z & -y \\ -z & 0 & x \\ y & -x & 0 \end{array} \right) \]](form_30.png)
.
Definition at line 887 of file geometry.h.
References ASSERT_.
Referenced by mrpt::poses::CPose3DRotVec::composeFrom(), jacob_dA_eps_D_p_deps(), mrpt::poses::CPose3D::jacob_dAexpeD_de(), jacob_deps_D_p_deps(), mrpt::poses::CPose3D::jacob_dexpeD_de(), and mrpt::math::vectorsAreParallel2D().
◆ skew_symmetric3_neg() [2/2]
|
inline |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
Definition at line 903 of file geometry.h.
◆ slerp() [1/3]
| void mrpt::math::slerp | ( | const CQuaternion< T > & | q0, |
| const CQuaternion< T > & | q1, | ||
| const double | t, | ||
| CQuaternion< T > & | q | ||
| ) |
SLERP interpolation between two quaternions.
- Parameters
-
[in] q0 The quaternion for t=0 [in] q1 The quaternion for t=1 [in] t A "time" parameter, in the range [0,1]. [out] q The output, interpolated quaternion.
- Template Parameters
-
T The type of the quaternion (e.g. float, double).
- Exceptions
-
std::exception Only in Debug, if t is not in the valid range.
Definition at line 35 of file slerp.h.
References ASSERTDEB_, and mrpt::math::square().
Referenced by mrpt::math::slerp(), mrpt::math::slerp_ypr(), and TEST().


◆ slerp() [2/3]
| void mrpt::mrpt::math::slerp | ( | const mrpt::poses::CPose3D & | q0, |
| const mrpt::poses::CPose3D & | q1, | ||
| const double | t, | ||
| mrpt::poses::CPose3D & | p | ||
| ) |
SLERP interpolation between two 6D poses - like mrpt::math::slerp for quaternions, but interpolates the [X,Y,Z] coordinates as well.
- Parameters
-
[in] p0 The pose for t=0 [in] p1 The pose for t=1 [in] t A "time" parameter, in the range [0,1]. [out] p The output, interpolated pose.
- Exceptions
-
std::exception Only in Debug, if t is not in the valid range.
Definition at line 20 of file slerp.cpp.
References mrpt::poses::CPose3D::getAsQuaternion(), mrpt::math::slerp(), mrpt::poses::CPoseOrPoint< DERIVEDCLASS >::x(), and mrpt::poses::CPoseOrPoint< DERIVEDCLASS >::y().
◆ slerp() [3/3]
| void mrpt::mrpt::math::slerp | ( | const mrpt::poses::CPose3DQuat & | q0, |
| const mrpt::poses::CPose3DQuat & | q1, | ||
| const double | t, | ||
| mrpt::poses::CPose3DQuat & | p | ||
| ) |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
Definition at line 34 of file slerp.cpp.
References mrpt::poses::CPose3DQuat::quat(), mrpt::math::slerp(), mrpt::poses::CPoseOrPoint< DERIVEDCLASS >::x(), and mrpt::poses::CPoseOrPoint< DERIVEDCLASS >::y().
◆ slerp_ypr()
| void mrpt::mrpt::math::slerp_ypr | ( | const mrpt::math::TPose3D & | q0, |
| const mrpt::math::TPose3D & | q1, | ||
| const double | t, | ||
| mrpt::math::TPose3D & | p | ||
| ) |
Definition at line 46 of file slerp.cpp.
References mrpt::math::TPose3D::getAsQuaternion(), mrpt::math::slerp(), and mrpt::math::UNINITIALIZED_QUATERNION.
Referenced by mrpt::poses::CPoseInterpolatorBase< 3 >::impl_interpolation(), and TEST().


◆ splitInConvexComponents() [1/2]
| bool mrpt::math::splitInConvexComponents | ( | const TPolygon2D & | poly, |
| std::vector< TPolygon2D > & | components | ||
| ) |
Splits a 2D polygon into convex components.
Definition at line 2389 of file geometry.cpp.
References cross(), mrpt::math::distance(), geometryEpsilon, mrpt::math::intersect(), mrpt::math::TPolygon2D::removeRedundantVertices(), TSegmentWithLine::segment, and mrpt::utils::sign().
Referenced by generatePolygon(), mrpt::opengl::CPolyhedron::makeConvexPolygons(), and mrpt::math::splitInConvexComponents().

◆ splitInConvexComponents() [2/2]
| bool mrpt::math::splitInConvexComponents | ( | const TPolygon3D & | poly, |
| std::vector< TPolygon3D > & | components | ||
| ) |
Splits a 3D polygon into convex components.
- Exceptions
-
std::logic_error if the polygon can't be fit into a plane.
Definition at line 2484 of file geometry.cpp.
References mrpt::math::TPolygon3D::getPlane(), mrpt::math::project3D(), and mrpt::math::splitInConvexComponents().
◆ traceRay() [1/2]
| bool mrpt::math::traceRay | ( | const std::vector< TPolygonWithPlane > & | vec, |
| const mrpt::poses::CPose3D & | pose, | ||
| double & | dist | ||
| ) |
Fast ray tracing method using polygons' properties.
- See also
- CRenderizable::rayTrace
Definition at line 2582 of file geometry.cpp.
References mrpt::math::createFromPoseX(), mrpt::math::intersect(), and mrpt::math::TLine3D::unitarize().
Referenced by mrpt::opengl::CTexturedPlane::traceRay(), mrpt::opengl::CGeneralizedCylinder::traceRay(), mrpt::opengl::CSetOfTriangles::traceRay(), mrpt::opengl::CMesh::traceRay(), and mrpt::opengl::CPolyhedron::traceRay().

◆ traceRay() [2/2]
|
inline |
Fast ray tracing method using polygons' properties.
- See also
- CRenderizable::rayTrace
Definition at line 789 of file geometry.h.
◆ vectorsAreParallel2D()
|
inline |
Returns true if two 2D vectors are parallel.
The arguments may be points, arrays, etc.
Definition at line 915 of file geometry.h.
References mrpt::math::skew_symmetric3_neg(), and mrpt::math::UNINITIALIZED_MATRIX.

◆ vectorsAreParallel3D()
|
inline |
Returns true if two 3D vectors are parallel.
The arguments may be points, arrays, etc.
Definition at line 925 of file geometry.h.
References mrpt::math::getEpsilon().

Variable Documentation
◆ GEOMETRIC_TYPE_LINE
| const unsigned char mrpt::math::GEOMETRIC_TYPE_LINE = 2 |
Object type identifier for TLine2D or TLine3D.
Definition at line 1571 of file lightweight_geom_data.h.
Referenced by fromObject(), mrpt::math::TObject3D::generate2DObject(), mrpt::math::TObject2D::generate3DObject(), mrpt::math::TObject2D::isLine(), mrpt::math::TObject3D::isLine(), mrpt::math::operator<<(), mrpt::math::TObject2D::operator=(), mrpt::math::TObject3D::operator=(), mrpt::math::operator>>(), mrpt::math::project2D(), and mrpt::math::project3D().
◆ GEOMETRIC_TYPE_PLANE
| const unsigned char mrpt::math::GEOMETRIC_TYPE_PLANE = 4 |
Object type identifier for TPlane.
- See also
- TObject3D
Definition at line 1581 of file lightweight_geom_data.h.
Referenced by mrpt::math::TObject3D::generate2DObject(), mrpt::math::TObject3D::isPlane(), mrpt::math::operator<<(), mrpt::math::TObject3D::operator=(), mrpt::math::operator>>(), and mrpt::math::project3D().
◆ GEOMETRIC_TYPE_POINT
| const unsigned char mrpt::math::GEOMETRIC_TYPE_POINT = 0 |
Object type identifier for TPoint2D or TPoint3D.
Definition at line 1561 of file lightweight_geom_data.h.
Referenced by fromObject(), mrpt::math::TObject3D::generate2DObject(), mrpt::math::TObject2D::generate3DObject(), mrpt::math::TObject2D::isPoint(), mrpt::math::TObject3D::isPoint(), mrpt::math::operator<<(), mrpt::math::TObject2D::operator=(), mrpt::math::TObject3D::operator=(), mrpt::math::operator>>(), mrpt::math::project2D(), mrpt::math::project3D(), and TEST().
◆ GEOMETRIC_TYPE_POLYGON
| const unsigned char mrpt::math::GEOMETRIC_TYPE_POLYGON = 3 |
Object type identifier for TPolygon2D or TPolygon3D.
Definition at line 1576 of file lightweight_geom_data.h.
Referenced by mrpt::math::TObject2D::destroy(), mrpt::math::TObject3D::destroy(), fromObject(), mrpt::math::TObject3D::generate2DObject(), mrpt::math::TObject2D::generate3DObject(), mrpt::math::TObject2D::isPolygon(), mrpt::math::TObject3D::isPolygon(), mrpt::math::operator<<(), mrpt::math::TObject2D::operator=(), mrpt::math::TObject3D::operator=(), mrpt::math::operator>>(), mrpt::math::project2D(), and mrpt::math::project3D().
◆ GEOMETRIC_TYPE_SEGMENT
| const unsigned char mrpt::math::GEOMETRIC_TYPE_SEGMENT = 1 |
Object type identifier for TSegment2D or TSegment3D.
Definition at line 1566 of file lightweight_geom_data.h.
Referenced by fromObject(), mrpt::math::TObject3D::generate2DObject(), mrpt::math::TObject2D::generate3DObject(), mrpt::math::TObject2D::isSegment(), mrpt::math::TObject3D::isSegment(), mrpt::math::operator<<(), mrpt::math::TObject2D::operator=(), mrpt::math::TObject3D::operator=(), mrpt::math::operator>>(), mrpt::math::project2D(), mrpt::math::project3D(), and TEST().
◆ GEOMETRIC_TYPE_UNDEFINED
| const unsigned char mrpt::math::GEOMETRIC_TYPE_UNDEFINED = 255 |
Object type identifier for empty TObject2D or TObject3D.
Definition at line 1586 of file lightweight_geom_data.h.
Referenced by mrpt::math::TObject2D::destroy(), mrpt::math::TObject3D::destroy(), mrpt::math::TObject3D::operator=(), and mrpt::math::operator>>().