Detailed Description

template<class T>
class mrpt::math::CQuaternion< T >

A quaternion, which can represent a 3D rotation as pair 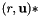$(r,\mathbf{u}) *$ , with a real part "r" and a 3D vector 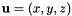$\mathbf{u} = (x,y,z)$ , or alternatively, q = r + ix + jy + kz.

The elements of the quaternion can be accessed by either:

r(), x(), y(), z(), or
the operator [] with indices running from 0 (=r) to 3 (=z).

Users will usually employ the type CQuaternionDouble instead of this template.

For more information about quaternions, see:

See also: mrpt::poses::CPose3D

Definition at line 44 of file CQuaternion.h.

#include <mrpt/math/CQuaternion.h>

Inheritance diagram for mrpt::math::CQuaternion< T >:

Public Types
using	value_type = T

Public Member Functions
T	r () const
	Return r coordinate of the quaternion. More...

T	x () const
	Return x coordinate of the quaternion. More...

T	y () const
	Return y coordinate of the quaternion. More...

T	z () const
	Return z coordinate of the quaternion. More...

void	r (const T r)
	Set r coordinate of the quaternion. More...

void	x (const T x)
	Set x coordinate of the quaternion. More...

void	y (const T y)
	Set y coordinate of the quaternion. More...

void	z (const T z)
	Set z coordinate of the quaternion. More...

template<class ARRAYLIKE3 >
void	fromRodriguesVector (const ARRAYLIKE3 &v)
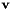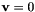	Set this quaternion to the rotation described by a 3D (Rodrigues) rotation vector $\mathbf{v}$ : If $\mathbf{v}=0$ , then the quaternion is $\mathbf{q} = [1 ~ 0 ~ 0 ~ 0]^\top$ , otherwise: $\mathbf{q} = \left[ \begin{array}{c} \cos(\frac{\theta}{2}) \\ v_x \frac{\sin(\frac{\theta}{2})}{\theta} \\ v_y \frac{\sin(\frac{\theta}{2})}{\theta} \\ v_z \frac{\sin(\frac{\theta}{2})}{\theta} \end{array} \right]$ where $\theta = \|\mathbf{v}\| = \sqrt{v_x^2+v_y^2+v_z^2}$ . More...

void	crossProduct (const CQuaternion &q1, const CQuaternion &q2)
	Calculate the "cross" product (or "composed rotation") of two quaternion: this = q1 x q2 After the operation, "this" will represent the composed rotations of q1 and q2 (q2 applied "after" q1). More...

void	rotatePoint (const double lx, const double ly, const double lz, double &gx, double &gy, double &gz) const
	Rotate a 3D point (lx,ly,lz) -> (gx,gy,gz) as described by this quaternion. More...

void	inverseRotatePoint (const double lx, const double ly, const double lz, double &gx, double &gy, double &gz) const
	Rotate a 3D point (lx,ly,lz) -> (gx,gy,gz) as described by the inverse (conjugate) of this quaternion. More...

double	normSqr () const
	Return the squared norm of the quaternion. More...

void	normalize ()
	Normalize this quaternion, so its norm becomes the unitity. More...

template<class MATRIXLIKE >
void	normalizationJacobian (MATRIXLIKE &J) const
	Calculate the 4x4 Jacobian of the normalization operation of this quaternion. More...

template<class MATRIXLIKE >
void	rotationJacobian (MATRIXLIKE &J) const
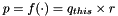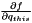	Compute the Jacobian of the rotation composition operation $p = f(\cdot) = q_{this} \times r$ , that is the 4x4 matrix $\frac{\partial f}{\partial q_{this} }$ . More...

template<class MATRIXLIKE >
void	rotationMatrix (MATRIXLIKE &M) const
	Calculate the 3x3 rotation matrix associated to this quaternion: $\mathbf{R} = \left( \begin{array}{ccc} q_r^2+q_x^2-q_y^2-q_z^2 & 2(q_x q_y - q_r q_z) & 2(q_z q_x+q_r q_y) \\ 2(q_x q_y+q_r q_z) & q_r^2-q_x^2+q_y^2-q_z^2 & 2(q_y q_z-q_r q_x) \\ 2(q_z q_x-q_r q_y) & 2(q_y q_z+q_r q_x) & q_r^2- q_x^2 - q_y^2 + q_z^2 \end{array} \right)$ . More...

template<class MATRIXLIKE >
void	rotationMatrixNoResize (MATRIXLIKE &M) const
	Fill out the top-left 3x3 block of the given matrix with the rotation matrix associated to this quaternion (does not resize the matrix, for that, see rotationMatrix). More...

void	conj (CQuaternion &q_out) const
	Return the conjugate quaternion. More...

CQuaternion	conj () const
	Return the conjugate quaternion. More...

void	rpy (T &roll, T &pitch, T &yaw) const
	Return the yaw, pitch & roll angles associated to quaternion. More...

template<class MATRIXLIKE >
void	rpy_and_jacobian (T &roll, T &pitch, T &yaw, MATRIXLIKE *out_dr_dq=nullptr, bool resize_out_dr_dq_to3x4=true) const
	Return the yaw, pitch & roll angles associated to quaternion, and (optionally) the 3x4 Jacobian of the transformation. More...

CQuaternion	operator* (const T &factor)


	CQuaternion (TConstructorFlags_Quaternions)
	Can be used with UNINITIALIZED_QUATERNION as argument, does not initialize the 4 elements of the quaternion (use this constructor when speed is critical). More...

	CQuaternion ()
	Default constructor: construct a (1, (0,0,0) ) quaternion representing no rotation. More...

	CQuaternion (const T r, const T x, const T y, const T z)
	Construct a quaternion from its parameters 'r', 'x', 'y', 'z', with q = r + ix + jy + kz. More...

Private Types
using	Base = CArrayNumeric< T, 4 >

Lie Algebra methods
template<class ARRAYLIKE3 >
void	ln (ARRAYLIKE3 &out_ln) const
	Logarithm of the 3x3 matrix defined by this pose, generating the corresponding vector in the SO(3) Lie Algebra, which coincides with the so-called "rotation vector" (I don't have space here for the proof ;-). More...

template<class ARRAYLIKE3 >
ARRAYLIKE3	ln () const
	overload that returns by value More...

template<class ARRAYLIKE3 >
void	ln_noresize (ARRAYLIKE3 &out_ln) const
	Like ln() but does not try to resize the output vector. More...

template<class ARRAYLIKE3 >
static CQuaternion< T >	exp (const ARRAYLIKE3 &v)
	Exponential map from the SO(3) Lie Algebra to unit quaternions. More...

template<class ARRAYLIKE3 >
static void	exp (const ARRAYLIKE3 &v, CQuaternion< T > &out_quat)

Member Typedef Documentation

◆ Base

template<class T>

using mrpt::math::CQuaternion< T >::Base = CArrayNumeric<T, 4>

private

Definition at line 46 of file CQuaternion.h.

◆ value_type

using mrpt::math::CArrayNumeric< T, N >::value_type = T

inherited

Definition at line 28 of file CArrayNumeric.h.

Constructor & Destructor Documentation

◆ CQuaternion() [1/3]

template<class T>

mrpt::math::CQuaternion< T >::CQuaternion ( TConstructorFlags_Quaternions )

inline

Can be used with UNINITIALIZED_QUATERNION as argument, does not initialize the 4 elements of the quaternion (use this constructor when speed is critical).

Definition at line 55 of file CQuaternion.h.

◆ CQuaternion() [2/3]

template<class T>

mrpt::math::CQuaternion< T >::CQuaternion ( )

inline

Default constructor: construct a (1, (0,0,0) ) quaternion representing no rotation.

Definition at line 58 of file CQuaternion.h.

◆ CQuaternion() [3/3]

template<class T>

mrpt::math::CQuaternion< T >::CQuaternion	(	const T	r,
		const T	x,
		const T	y,
		const T	z
	)

inline

Construct a quaternion from its parameters 'r', 'x', 'y', 'z', with q = r + ix + jy + kz.

Definition at line 68 of file CQuaternion.h.

References ASSERTMSG_, mrpt::format(), mrpt::math::CQuaternion< T >::normSqr(), mrpt::math::CQuaternion< T >::r(), mrpt::math::CQuaternion< T >::x(), mrpt::math::CQuaternion< T >::y(), and mrpt::math::CQuaternion< T >::z().

Member Function Documentation

◆ conj() [1/2]

template<class T>

void mrpt::math::CQuaternion< T >::conj ( CQuaternion< T > & q_out ) const

inline

Return the conjugate quaternion.

Definition at line 372 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::r(), mrpt::math::CQuaternion< T >::x(), mrpt::math::CQuaternion< T >::y(), and mrpt::math::CQuaternion< T >::z().

Referenced by mrpt::poses::CPose3DQuatPDFGaussianInf::inverse(), and mrpt::poses::CPose3DQuatPDFGaussian::inverse().

◆ conj() [2/2]

template<class T>

CQuaternion mrpt::math::CQuaternion< T >::conj ( ) const

inline

Return the conjugate quaternion.

Definition at line 381 of file CQuaternion.h.

◆ crossProduct()

template<class T>

void mrpt::math::CQuaternion< T >::crossProduct	(	const CQuaternion< T > &	q1,
		const CQuaternion< T > &	q2
	)

inline

Calculate the "cross" product (or "composed rotation") of two quaternion: this = q1 x q2 After the operation, "this" will represent the composed rotations of q1 and q2 (q2 applied "after" q1).

Definition at line 200 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::normalize(), mrpt::math::CQuaternion< T >::r(), mrpt::math::CQuaternion< T >::x(), mrpt::math::CQuaternion< T >::y(), and mrpt::math::CQuaternion< T >::z().

Referenced by mrpt::poses::CPose3DQuat::composeFrom(), mrpt::poses::CPose3DQuat::inverseComposeFrom(), mrpt::poses::CPose3DPDF::jacobiansPoseComposition(), and TEST_F().

◆ exp() [1/2]

template<class T>

template<class ARRAYLIKE3 >

static CQuaternion<T> mrpt::math::CQuaternion< T >::exp ( const ARRAYLIKE3 & v )

inlinestatic

Exponential map from the SO(3) Lie Algebra to unit quaternions.

See also: ln, mrpt::poses::SE_traits

Definition at line 180 of file CQuaternion.h.

References mrpt::math::UNINITIALIZED_QUATERNION.

◆ exp() [2/2]

template<class T>

template<class ARRAYLIKE3 >

static void mrpt::math::CQuaternion< T >::exp	(	const ARRAYLIKE3 &	v,
		CQuaternion< T > &	out_quat
	)

inlinestatic

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

Definition at line 188 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::fromRodriguesVector().

◆ fromRodriguesVector()

template<class T>

template<class ARRAYLIKE3 >

void mrpt::math::CQuaternion< T >::fromRodriguesVector ( const ARRAYLIKE3 & v )

inline

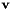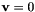Set this quaternion to the rotation described by a 3D (Rodrigues) rotation vector $\mathbf{v}$ : If $\mathbf{v}=0$ , then the quaternion is $\mathbf{q} = [1 ~ 0 ~ 0 ~ 0]^\top$ , otherwise:

$\mathbf{q} = \left[ \begin{array}{c} \cos(\frac{\theta}{2}) \\ v_x \frac{\sin(\frac{\theta}{2})}{\theta} \\ v_y \frac{\sin(\frac{\theta}{2})}{\theta} \\ v_z \frac{\sin(\frac{\theta}{2})}{\theta} \end{array} \right]$

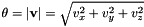where $\theta = |\mathbf{v}| = \sqrt{v_x^2+v_y^2+v_z^2}$ .

See also: "Representing Attitude: Euler Angles, Unit Quaternions, and Rotation Vectors (2006)", James Diebel.

Definition at line 115 of file CQuaternion.h.

References THROW_EXCEPTION, mrpt::math::CQuaternion< T >::x(), mrpt::math::CQuaternion< T >::y(), and mrpt::math::CQuaternion< T >::z().

Referenced by mrpt::math::CQuaternion< T >::exp().

◆ inverseRotatePoint()

template<class T>

void mrpt::math::CQuaternion< T >::inverseRotatePoint	(	const double	lx,
		const double	ly,
		const double	lz,
		double &	gx,
		double &	gy,
		double &	gz
	)		const

inline

Rotate a 3D point (lx,ly,lz) -> (gx,gy,gz) as described by the inverse (conjugate) of this quaternion.

Definition at line 243 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::r(), mrpt::math::CQuaternion< T >::x(), mrpt::math::CQuaternion< T >::y(), and mrpt::math::CQuaternion< T >::z().

Referenced by mrpt::poses::CPose3DQuat::inverseComposePoint().

◆ ln() [1/2]

template<class T>

template<class ARRAYLIKE3 >

void mrpt::math::CQuaternion< T >::ln ( ARRAYLIKE3 & out_ln ) const

inline

Logarithm of the 3x3 matrix defined by this pose, generating the corresponding vector in the SO(3) Lie Algebra, which coincides with the so-called "rotation vector" (I don't have space here for the proof ;-).

Parameters

[out] out_ln The target vector, which can be: std::vector<>, or mrpt::math::CVectorDouble or any row or column Eigen::Matrix<>.

See also: exp, mrpt::poses::SE_traits

Definition at line 152 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::ln_noresize().

Referenced by QuaternionTests::test_ExpAndLnMatches(), and QuaternionTests::test_lnAndExpMatches().

◆ ln() [2/2]

template<class T>

template<class ARRAYLIKE3 >

ARRAYLIKE3 mrpt::math::CQuaternion< T >::ln ( ) const

inline

overload that returns by value

Definition at line 159 of file CQuaternion.h.

◆ ln_noresize()

template<class T>

template<class ARRAYLIKE3 >

void mrpt::math::CQuaternion< T >::ln_noresize ( ARRAYLIKE3 & out_ln ) const

inline

Like ln() but does not try to resize the output vector.

Definition at line 167 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::r(), mrpt::square(), mrpt::math::CQuaternion< T >::x(), mrpt::math::CQuaternion< T >::y(), and mrpt::math::CQuaternion< T >::z().

Referenced by mrpt::math::CQuaternion< T >::ln().

◆ normalizationJacobian()

template<class T>

template<class MATRIXLIKE >

void mrpt::math::CQuaternion< T >::normalizationJacobian ( MATRIXLIKE & J ) const

inline

Calculate the 4x4 Jacobian of the normalization operation of this quaternion.

The output matrix can be a dynamic or fixed size (4x4) matrix.

Definition at line 281 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::normSqr(), mrpt::math::CQuaternion< T >::r(), mrpt::math::CQuaternion< T >::x(), mrpt::math::CQuaternion< T >::y(), and mrpt::math::CQuaternion< T >::z().

Referenced by mrpt::poses::CPose3DQuat::composePoint(), mrpt::poses::CPose3DPDFGaussian::copyFrom(), mrpt::poses::CPose3DQuat::inverseComposePoint(), mrpt::poses::CPose3DQuatPDF::jacobiansPoseComposition(), mrpt::poses::CPose3DPDF::jacobiansPoseComposition(), and Pose3DQuatTests::test_normalizeJacob().

◆ normalize()

template<class T>

void mrpt::math::CQuaternion< T >::normalize ( )

inline

Normalize this quaternion, so its norm becomes the unitity.

Definition at line 270 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::normSqr().

Referenced by mrpt::poses::CPose3DQuat::CPose3DQuat(), and mrpt::math::CQuaternion< T >::crossProduct().

◆ normSqr()

template<class T>

double mrpt::math::CQuaternion< T >::normSqr ( ) const

inline

Return the squared norm of the quaternion.

Definition at line 262 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::r(), mrpt::square(), mrpt::math::CQuaternion< T >::x(), mrpt::math::CQuaternion< T >::y(), and mrpt::math::CQuaternion< T >::z().

Referenced by mrpt::math::CQuaternion< T >::CQuaternion(), mrpt::math::CQuaternion< T >::normalizationJacobian(), and mrpt::math::CQuaternion< T >::normalize().

◆ operator*()

template<class T>

CQuaternion mrpt::math::CQuaternion< T >::operator* ( const T & factor )

inline

Definition at line 491 of file CQuaternion.h.

◆ r() [1/2]

template<class T>

T mrpt::math::CQuaternion< T >::r ( ) const

inline

Return r coordinate of the quaternion.

Definition at line 85 of file CQuaternion.h.

◆ r() [2/2]

template<class T>

void mrpt::math::CQuaternion< T >::r ( const T r )

inline

Set r coordinate of the quaternion.

Definition at line 93 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::r().

◆ rotatePoint()

template<class T>

void mrpt::math::CQuaternion< T >::rotatePoint	(	const double	lx,
		const double	ly,
		const double	lz,
		double &	gx,
		double &	gy,
		double &	gz
	)		const

inline

Rotate a 3D point (lx,ly,lz) -> (gx,gy,gz) as described by this quaternion.

Definition at line 222 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::r(), mrpt::math::CQuaternion< T >::x(), mrpt::math::CQuaternion< T >::y(), and mrpt::math::CQuaternion< T >::z().

Referenced by mrpt::poses::CPose3DQuat::composeFrom(), mrpt::poses::CPose3DQuat::composePoint(), and mrpt::poses::CPose3DQuat::inverseComposeFrom().

◆ rotationJacobian()

template<class T>

template<class MATRIXLIKE >

void mrpt::math::CQuaternion< T >::rotationJacobian ( MATRIXLIKE & J ) const

inline

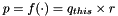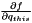Compute the Jacobian of the rotation composition operation $p = f(\cdot) = q_{this} \times r$ , that is the 4x4 matrix $\frac{\partial f}{\partial q_{this} }$ .

The output matrix can be a dynamic or fixed size (4x4) matrix.

Definition at line 313 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::r(), mrpt::math::CQuaternion< T >::x(), mrpt::math::CQuaternion< T >::y(), and mrpt::math::CQuaternion< T >::z().

◆ rotationMatrix()

template<class T>

template<class MATRIXLIKE >

void mrpt::math::CQuaternion< T >::rotationMatrix ( MATRIXLIKE & M ) const

inline

Calculate the 3x3 rotation matrix associated to this quaternion:

$\mathbf{R} = \left( \begin{array}{ccc} q_r^2+q_x^2-q_y^2-q_z^2 & 2(q_x q_y - q_r q_z) & 2(q_z q_x+q_r q_y) \\ 2(q_x q_y+q_r q_z) & q_r^2-q_x^2+q_y^2-q_z^2 & 2(q_y q_z-q_r q_x) \\ 2(q_z q_x-q_r q_y) & 2(q_y q_z+q_r q_x) & q_r^2- q_x^2 - q_y^2 + q_z^2 \end{array} \right)$

.

Definition at line 348 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::rotationMatrixNoResize().

◆ rotationMatrixNoResize()

template<class T>

template<class MATRIXLIKE >

void mrpt::math::CQuaternion< T >::rotationMatrixNoResize ( MATRIXLIKE & M ) const

inline

Fill out the top-left 3x3 block of the given matrix with the rotation matrix associated to this quaternion (does not resize the matrix, for that, see rotationMatrix).

Definition at line 358 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::r(), mrpt::math::CQuaternion< T >::x(), mrpt::math::CQuaternion< T >::y(), and mrpt::math::CQuaternion< T >::z().

Referenced by mrpt::poses::CPose3DQuat::getHomogeneousMatrix(), and mrpt::math::CQuaternion< T >::rotationMatrix().

◆ rpy()

template<class T>

void mrpt::math::CQuaternion< T >::rpy	(	T &	roll,
		T &	pitch,
		T &	yaw
	)		const

inline

Return the yaw, pitch & roll angles associated to quaternion.

See also: For the equations, see The MRPT Book, or see http://www.euclideanspace.com/maths/geometry/rotations/conversions/quaternionToEuler/Quaternions.pdf; rpy_and_jacobian

Definition at line 393 of file CQuaternion.h.

References mrpt::obs::gnss::pitch, mrpt::obs::gnss::roll, and mrpt::math::CQuaternion< T >::rpy_and_jacobian().

Referenced by mrpt::poses::internal::getPoseFromString().

◆ rpy_and_jacobian()

template<class T>

template<class MATRIXLIKE >

void mrpt::math::CQuaternion< T >::rpy_and_jacobian	(	T &	roll,
		T &	pitch,
		T &	yaw,
		MATRIXLIKE *	out_dr_dq = `nullptr`,
		bool	resize_out_dr_dq_to3x4 = `true`
	)		const

inline

Return the yaw, pitch & roll angles associated to quaternion, and (optionally) the 3x4 Jacobian of the transformation.

Note that both the angles and the Jacobian have one set of normal equations, plus other special formulas for the degenerated cases of |pitch|=90 degrees.

See also: For the equations, see The MRPT Book, or http://www.euclideanspace.com/maths/geometry/rotations/conversions/quaternionToEuler/Quaternions.pdf; rpy

Definition at line 409 of file CQuaternion.h.

References M_PI, mrpt::obs::gnss::pitch, mrpt::math::CQuaternion< T >::r(), mrpt::obs::gnss::roll, mrpt::square(), mrpt::math::CQuaternion< T >::x(), mrpt::math::CQuaternion< T >::y(), and mrpt::math::CQuaternion< T >::z().

Referenced by mrpt::poses::CPose3DPDFGaussian::copyFrom(), mrpt::poses::CPose3DPDF::jacobiansPoseComposition(), and mrpt::math::CQuaternion< T >::rpy().

◆ x() [1/2]

template<class T>

T mrpt::math::CQuaternion< T >::x ( ) const

inline

Return x coordinate of the quaternion.

Definition at line 87 of file CQuaternion.h.

◆ x() [2/2]

template<class T>

void mrpt::math::CQuaternion< T >::x ( const T x )

inline

Set x coordinate of the quaternion.

Definition at line 95 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::x().

◆ y() [1/2]

template<class T>

T mrpt::math::CQuaternion< T >::y ( ) const

inline

Return y coordinate of the quaternion.

Definition at line 89 of file CQuaternion.h.

◆ y() [2/2]

template<class T>

void mrpt::math::CQuaternion< T >::y ( const T y )

inline

Set y coordinate of the quaternion.

Definition at line 97 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::y().

◆ z() [1/2]

template<class T>

T mrpt::math::CQuaternion< T >::z ( ) const

inline

Return z coordinate of the quaternion.

Definition at line 91 of file CQuaternion.h.

◆ z() [2/2]

template<class T>

void mrpt::math::CQuaternion< T >::z ( const T z )

inline

Set z coordinate of the quaternion.

Definition at line 99 of file CQuaternion.h.

References mrpt::math::CQuaternion< T >::z().

Detailed Description

template<class T> class mrpt::math::CQuaternion< T >

Public Types

Public Member Functions

Private Types

Lie Algebra methods

Member Typedef Documentation

◆ Base

◆ value_type

Constructor & Destructor Documentation

◆ CQuaternion() [1/3]

◆ CQuaternion() [2/3]

◆ CQuaternion() [3/3]

Member Function Documentation

◆ conj() [1/2]

◆ conj() [2/2]

◆ crossProduct()

◆ exp() [1/2]

◆ exp() [2/2]

◆ fromRodriguesVector()

◆ inverseRotatePoint()

◆ ln() [1/2]

◆ ln() [2/2]

◆ ln_noresize()

◆ normalizationJacobian()

◆ normalize()

◆ normSqr()

◆ operator*()

◆ r() [1/2]

◆ r() [2/2]

◆ rotatePoint()

◆ rotationJacobian()

◆ rotationMatrix()

◆ rotationMatrixNoResize()

◆ rpy()

◆ rpy_and_jacobian()

◆ x() [1/2]

◆ x() [2/2]

◆ y() [1/2]

◆ y() [2/2]

◆ z() [1/2]

◆ z() [2/2]

template<class T>
class mrpt::math::CQuaternion< T >